Voice typo?
-
At timestamp 1:10 it seemed like Prof. Loh just repeated what he said. Also when or where can I find proof of why inscribed angles= 1/2 the angles they inscribe? I forgot sorry.
-
@The-Darkin-Blade Hi there!
Thank you for mentioning about this voice typo! We will definitely take a look and think about what to do about it!
Now, let me answer your question about inscribed angles.
The formal wording of this theorem goes like this:
Inscribed Angle Theorem:
Any angle that is inscribed in a circle is half of the central angle that subtends the same arc on the circle.
Proof:
Let our inscribed angle be \(\angle BAC\) and the central angle \(\angle BOC.\)
There are two cases for the position of the inscribed angle relative to the central angle.
Case 1:
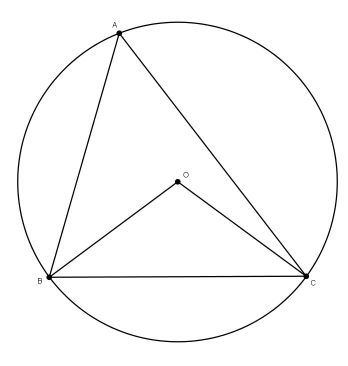
Let's draw one more radius, \(\overline{OA}.\) Now we have three isosceles triangles: \(\bigtriangleup AOB,\) \(\bigtriangleup AOC\) and \(\bigtriangleup BOC.\) So the the angles at the base are equal. Let \(\alpha = \angle BAO=\angle ABO,\) \(\beta = \angle CAO=\angle ACO\) and \(\gamma= \angle BCO=\angle CBO.\) So the \(\angle BAC = \alpha+\beta.\)
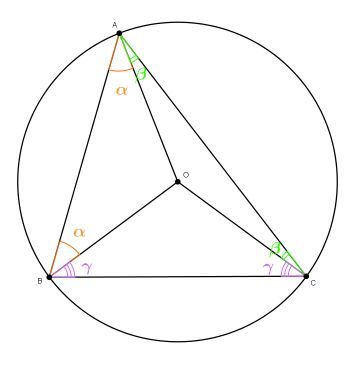
Let's now find the measure of the angle \(\angle BOC:\)
The sum of the angles in any triangle is equal to \(180^{\circ},\) so \(\angle BOC=180^{\circ}-2\gamma\) and also \(\angle BAC+\angle ABC+\angle ACB=180^{\circ}.\)
On the other hand, \(\text{sum of the angles in }\triangle ABC=2\alpha+2\beta+2\gamma=180^{\circ},\) hence \(2\alpha+2\beta = 180^{\circ}-2\gamma=\angle BOC.\) And we got what we wanted: \(\angle BOC=2\alpha+2\beta=2(\alpha+\beta)=2\angle BAC.\)
So we are done!
Case 2:
Now, if you want, you can try to prove this case yourself, using the ideas from the proof of the first case
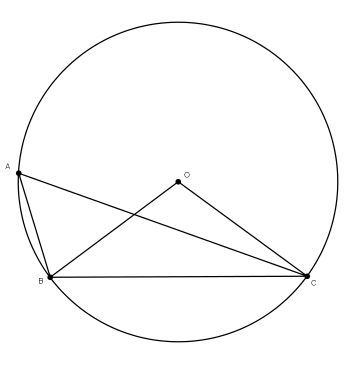
Let's draw one more radius, \(\overline{OA}.\) Now we have three isosceles triangles: \(\bigtriangleup AOB,\) \(\bigtriangleup AOC\) and \(\bigtriangleup BOC.\) So the angles at the base are equal. Let \(\alpha = \angle BAO=\angle ABO,\) \(\beta = \angle CAO=\angle ACO\) and \(\gamma= \angle BCO=\angle CBO.\) So the \(\angle BAC = \alpha-\beta.\)

Let's now find the measure of the angle \(\angle BOC:\)
The sum of the angles in any triangle is equal to \(180^{\circ},\) so \(\angle BOC=180^{\circ}-2\gamma\) and also \(\angle BAC+\angle ABC+\angle ACB=180^{\circ}.\)
On the other hand, \(\text{sum of the angles in }\triangle ABC=(\alpha-\beta)+(\alpha+\gamma)+(\gamma-\beta) = 2\alpha-2\beta+2\gamma=180^{\circ},\) hence \(2\alpha-2\beta = 180^{\circ}-2\gamma=\angle BOC.\) And we got what we wanted: \(\angle BOC=2\alpha-2\beta=2(\alpha-\beta)=2\angle BAC.\)
So we are done again, using the same algorithm! -
@nastya \(\bigtriangleup ACO \)