How can we prove that the formula works for all polygons?
-
How can we prove that the formula (shown in the lesson) works for all polygons?
-
Hey @professionalbronco ! Sorry for getting to you so late,
It actually doesn't -- in order to use the method shown, you have to be able to inscribe a circle perfectly inside the polygon. Or in other words, you have to be able to draw altitudes of exactly the same length to all of the sides from one point. Look at this long hexagon for example:

If I took the center of this hexagon and drew altitudes, it wouldn't work! The altitudes to the diagonal sides go outside the hexagon (because remember, they have to intersect at an exactly \(90^{\circ}\) angle), and those altitudes are much longer than the altitudes to the horizontal sides. But, you can still use the same idea! By dividing up the hexagon into a bunch of tinier triangles, you can find the area that way, just not simply \(\frac12 \cdot r \cdot p \). This is actually a very good strategy in general. If you can't find the area of a weird shape, try dividing it into smaller shapes that you can find the area of.
So, let's look at shapes that we can inscribe a circle in. Regular polygons are a great example. Regular just means that the polygon is equilateral and equiangular. And, in every regular polygon, we can inscribe a circle. If we were to take a regular hexagon, the radius of the incircle would look something like this:
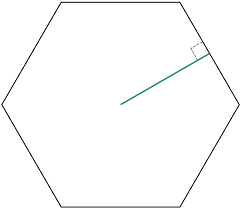
Let's call the side length of the hexagon \(s\) and the green line \(r\). Then, after splitting the hexagon into 6 smaller triangles, the area of every triangle is just \(\frac12 \cdot r \cdot s\).

So the area of the whole hexagon is \(\frac12 \cdot r \cdot s\) + \(\frac12 \cdot r \cdot s\) + \(\frac12 \cdot r \cdot s\) + \(\frac12 \cdot r \cdot s\) + \(\frac12 \cdot r \cdot s\) + \(\frac12 \cdot r \cdot s\). I know I could've just written it as \(\frac12 \cdot r \cdot s \cdot 6\), but keeping it this way can help make sense of why it works for every polygon with an inscribed circle:
If we factor out \(\frac12 \cdot r \), we get that the area is equal to \(\frac12 \cdot r \cdot (s+s+s+s+s+s)\). And the expression inside the parentheses is just the perimeter of the hexagon! So, \(A= \frac12 \cdot r \cdot p \).
And in general, for any other polygon with an inscribed circle, the expression inside the parenthesis will just be the perimeter. This proves it!
Note: for regular polygons only, the radius of the inscribed circle is actually just a line going from the center of the polygon to the midpoint of one of its sides (like the green line in the hexagon image). So, sometimes you will see the word apothem, which is exactly that. For regular polygons you might come across \(A = \frac12 \cdot a \cdot p \), which is exactly the same formula but specifically for just regular polygons.
-
@quacker88 What if we don't have a regular polygon? How can we tell if we can inscribe a circle in it?
-
@professionalbronco All triangles can be inscribed in a circle and I think all quadrilaterals whose opposite angles add up to 180 (because of the arcs and stuff) called 'cyclic quadrilaterals' can be inscribed inside a circle too...
yeah idk about polygons with more sides tho X)
-
@professionalbronco That's a little more difficult. Sometimes, the problem will literally just involve a circle and a polygon, and in that case, great! But also, @energizedpanda is right. You can always inscribe a circle in any triangle (called the incircle). And for quadrilaterals, if you can inscribe a circle inside, those are called cyclic quadrilaterals. One great way to test if a quadrilateral is cyclic is exactly what energizedpanda said, if the opposite angles add up to \(180^{\circ}\), then it's cyclic. There are other methods too that you can search up if you want, but that's usually the simplest test.
For polygons with more than five sides though... good luck. Usually there's probably some other way, like dividing up the shape into smaller shapes or thinking outside the box. But, you can always consider inscribing a circle if you know it's 100% possible!
Hope this helps

-
@energizedpanda @quacker88 Thanks!