An easier way to do Final Review Q17
-
Final Review Q17 asks :
An isosceles triangle has sides of AB=2028, AC=2028, and BC=2856. There are two inscribed circles with the same radius, both internally tangent to the triangle along BCWhat is the length of the radius of the circles?
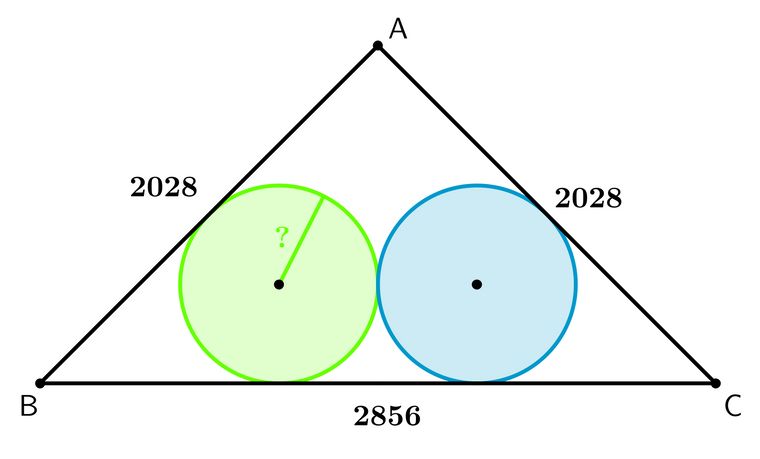
My solution:
First you split the triangle vertically through the middle to for two right triangles.

Next you note that the 2 right triangles are 119-120-169 triangles scaled up by 12. For now we can ignore the factor of 12.
Third you also note that one formula for the area of a triangle is A=rs.
Fourth you find the area of a 119-120-169 right triangle by using A=bh/2=119(120)/2=7140.
Fifth you find the semiperimeter: 119+120+169/2=204.
Sixth you find the inradius by dividing the area 7140 by the semiperimeter 204. The inradius is 35.
Lastly don't forget to scale the inradius back up by multiplying it by 12! 35x12=420.
So the answer is 420.
-
@iamnotawhale Way to go!! That's a pretty fast solution, nice job for thinking about A = rs.