In this mini question, why does choice ii not work?
-
Module 2 Day 7 Challenge Part 4 Mini-Question
In this mini question, why does choice ii not work?
-
@carefulunicorn-0 Hi carefulunicorn! Thank you for asking! This is interesting, and it relies on some tiny little details of the wording of the answer choice ii.).
Let's take a look at answer choice ii.) again.
"The radius is an integer \(\textcolor{red}{\text{only if}}\) the length of \(\overline{AB}\) is a square."
The wording "\(\textcolor{red}{\text{only if}}\)" when used like "\(A\) is true \(\textcolor{red}{\text{only if}}\) \(B\) is true" means that when \(B\) isn't true, then \(A\) shouldn't be true, either. The set of possible \(A\) lies inside the set of possible \(B.\)
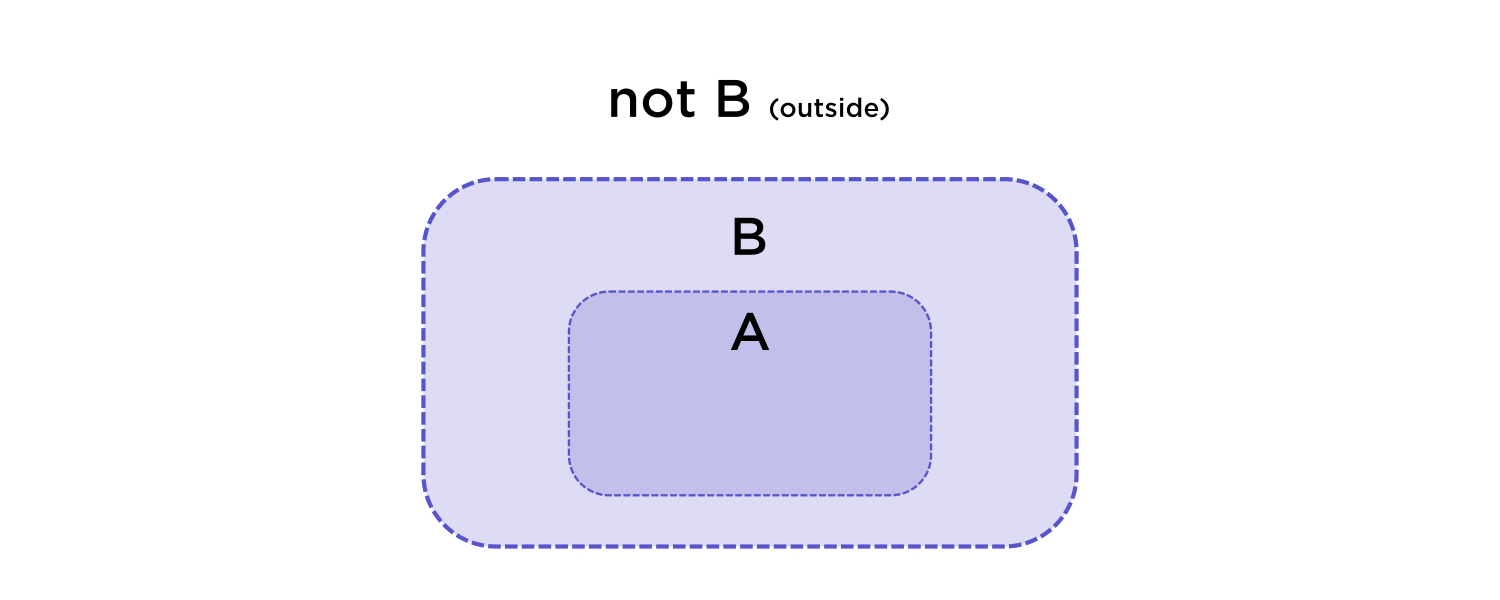
We can match the pieces of our statement to the conditions \(A\) and \(B\).
$$ A = \text{ radius is an integer} $$
$$ B = \overline{AB} \text{ is a square} $$
So, using this logic idea, if we \(\textcolor{blue}{\text{don't}}\) have \(B\) true, then \(A\) can't be true either. If \(\overline{AB}\) is \( \textcolor{red}{\text{not}}\) a square, then the radius \(\textcolor{red}{\text{can't}}\) be an integer.
Oh, but I can find a counterexample case where this statement isn't true, where \(\overline{AB}\) isn't a square, but the radius is still an integer!
Take a look here: If I construct a \(3-4-5\) right triangle like the one below, then the length of \(AB\) is \(10,\) which isn't a square, but the radius is \(4,\) which is an integer!
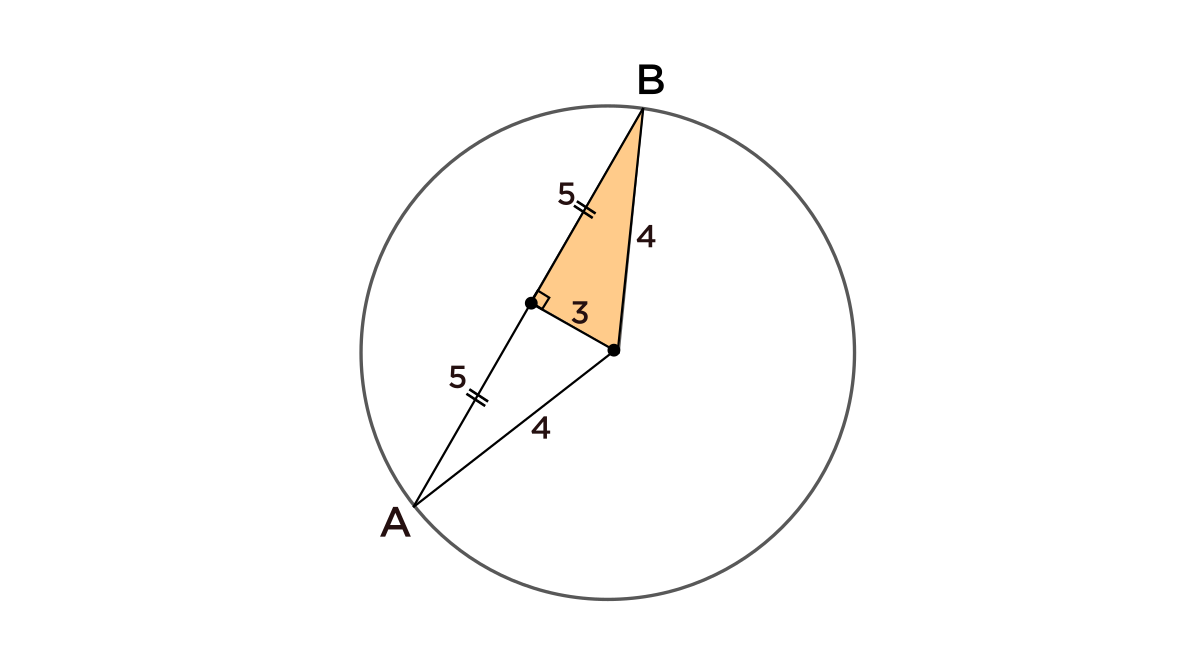
"But can one counterexample just prove that a statement is wrong?"
Well, yes! The funny thing about math is that it's quite easy to show that a statement is wrong, by just providing an example that fits all of the conditions except for one, and show that that last condition isn't true. It's much harder to prove that things are true rather than that things are true.
It's like that quote from Anna Karenina, by Leo Tolstoy,
$$ \text{ All happy families are alike, but every unhappy family is unhappy in its own way. } $$

-
@debbie thank you!