Why is ⅓ = 0.3333....?
-
Why is it true that \(\frac{1}{3} = 0.\overline{333}\ldots \) ?
I wish I had a very simple and clever way to show this, but all the simple and clever ways usually use some idea that is already a step more advanced.
For example, you could say that \( 0.\overline{999}\ldots = 1\) and then divide both sides by \(3\) (but knowing the fact that \(0.\overline{999}\ldots = 1 \) is even harder to prove!). 
Or you could start from the fact that \(0.\overline{111}\ldots = \frac{1}{9}\) and multiply both sides by \(3,\) but wait, isn't that just the reverse of what we did to get to this place? 
We were originally trying to show \(\frac{1}{9} = 0.\overline{111}\ldots\) in the first place, assuming that we knew the decimal representation of \(\frac{1}{3}!\) 
(Round and round we go!)I think the best way to show why \(\frac{1}{3} = 0.\overline{333}\ldots \) is just to show the long division. Then you'll find that \(1\) divided by \(3\) equals \(0.\overline{333}\ldots.\) . This isn't hard, but there are some basic concepts to lay down first.
: place value and the idea of division as a reverse-multiplication operation. 
Place value
I have some affectionate names that I personally like to use when referring to place value digits. You can make up your own names, or you can use the standard names! It doesn't really matter what the names are, as long as you understand how they relate to each other.
$$ \textcolor{red}{1}.2345\ldots $$
In the number above, the \(\textcolor{red}{1}\) can be drawn as one "dot," or, in the standard terminology, a "one."
If you magnify a dot so that it looks bigger and bigger, you'll see that it's made up of 10 slices. (The standard terminology is "tenths.")
$$ 1.\textcolor{red}{2}345\ldots $$
In the decimal above, the \(\textcolor{red}{2 \text{ slices}}\) are highlighted in red. Any digit in this position, directly to the right of the decimal point, counts the number of \(\textcolor{red}{ \text{ slices}}\) in our number.
How about one slice? Well, since we're using the decimal system, everything is packaged in groups of \(10,\) so it makes sense that one \(\textcolor{red}{ \text{ slice}}\) would consist of \(\textcolor{red}{ 10 \text{ slivers.}}\)
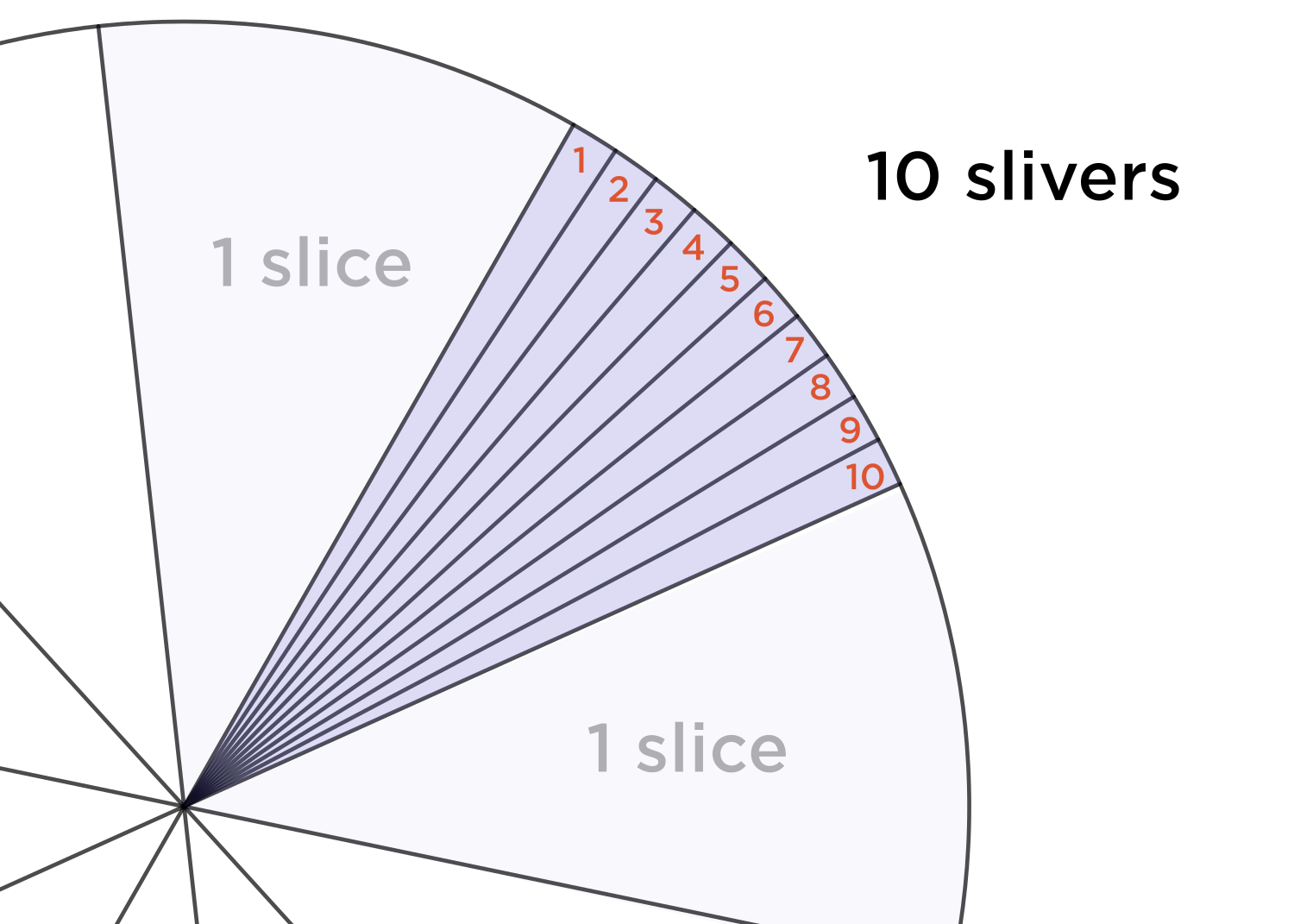
$$1.2 \textcolor{red}{3}45\ldots $$
In the number above, the \(\textcolor{red}{3}\) can be illustrated as \(3\) \(\textcolor{red}{\text{slivers.}}\)
It might be easier to imagine rather than to draw out what one \(\textcolor{red}{ \text{ sliver}}\) would consist of. It would consist of \(10\) quite skinny bits.... for lack a better word, I will call them here \(\textcolor{red}{ \text{ hairs}.}\)
The beautiful imagery of math.$$1.23 \textcolor{red}{4}5\ldots $$
In the number above, the \(\textcolor{red}{4}\) can be illustrated as \(\textcolor{red}{4 \text{ hairs.}}\)
All you have to remember is that in our decimal system, everything comes in groups of \(10.\)
Now we're all set to divide \(\frac{1}{3}!\)
The meaning of division
It might be good to review this a little bit. After all, \(\frac{1}{3}\) really just means \(1\) divided by \(3.\) Let's take a a look at another simple times.
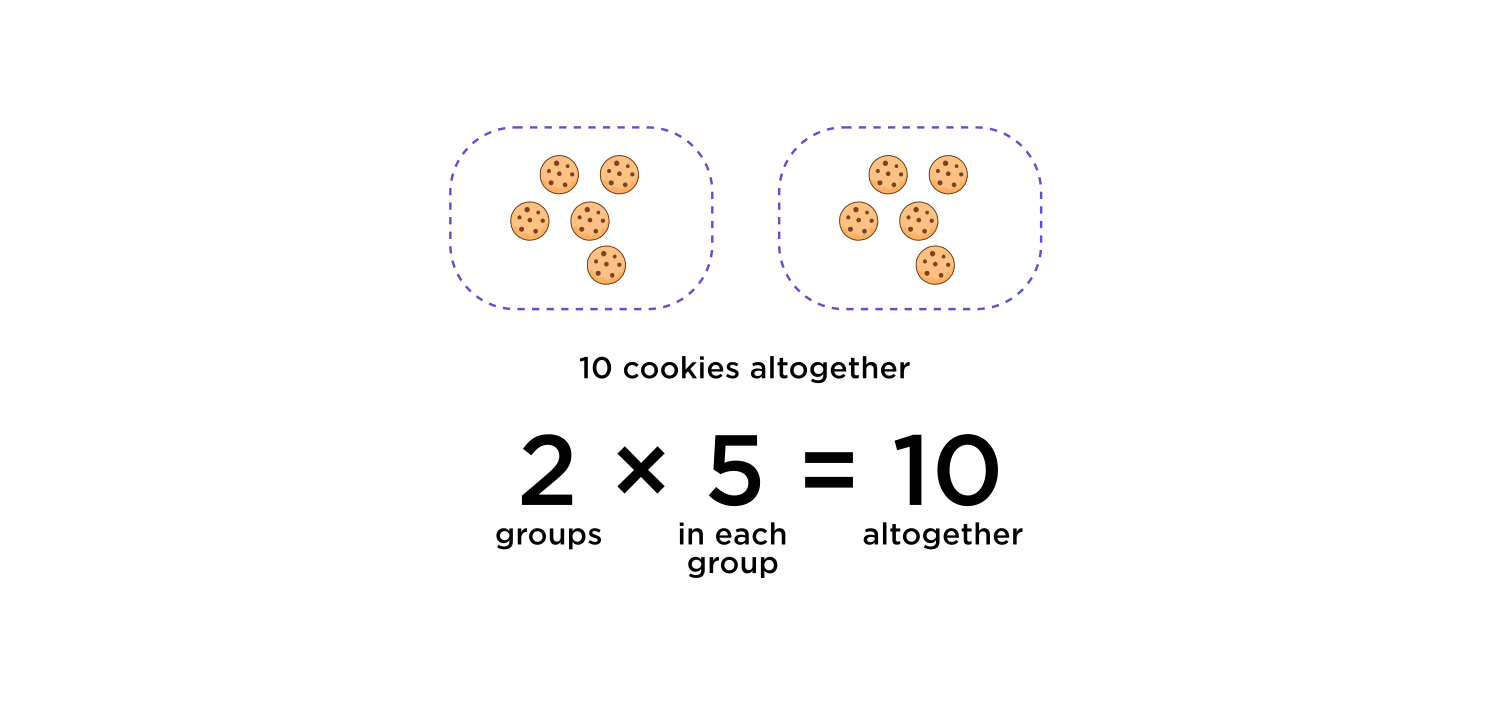
$$ \textcolor{blue}{2} \times \textcolor{green}{5} = \textcolor{purple}{10} $$
Here the \( \textcolor{blue}{\text{blue } 2}\) means \( \textcolor{blue}{2 \text{ groups}} \) , and the \( \textcolor{green}{\text{ green } 5}\) means how many things are \( \textcolor{green}{\text{ in each group. } }\) The last number, \( \textcolor{purple}{10,}\) means \( \textcolor{purple}{ \text{ how many things there are altogether. } }\)
$$ \textcolor{blue}{2 \text{ groups } } \times \textcolor{green}{5 \text{ in each group } } = \textcolor{purple}{10 \text{ altogether} } $$
Even if we divide both sides by \( \textcolor{blue}{ 2}\), the meanings of these parts is the same.
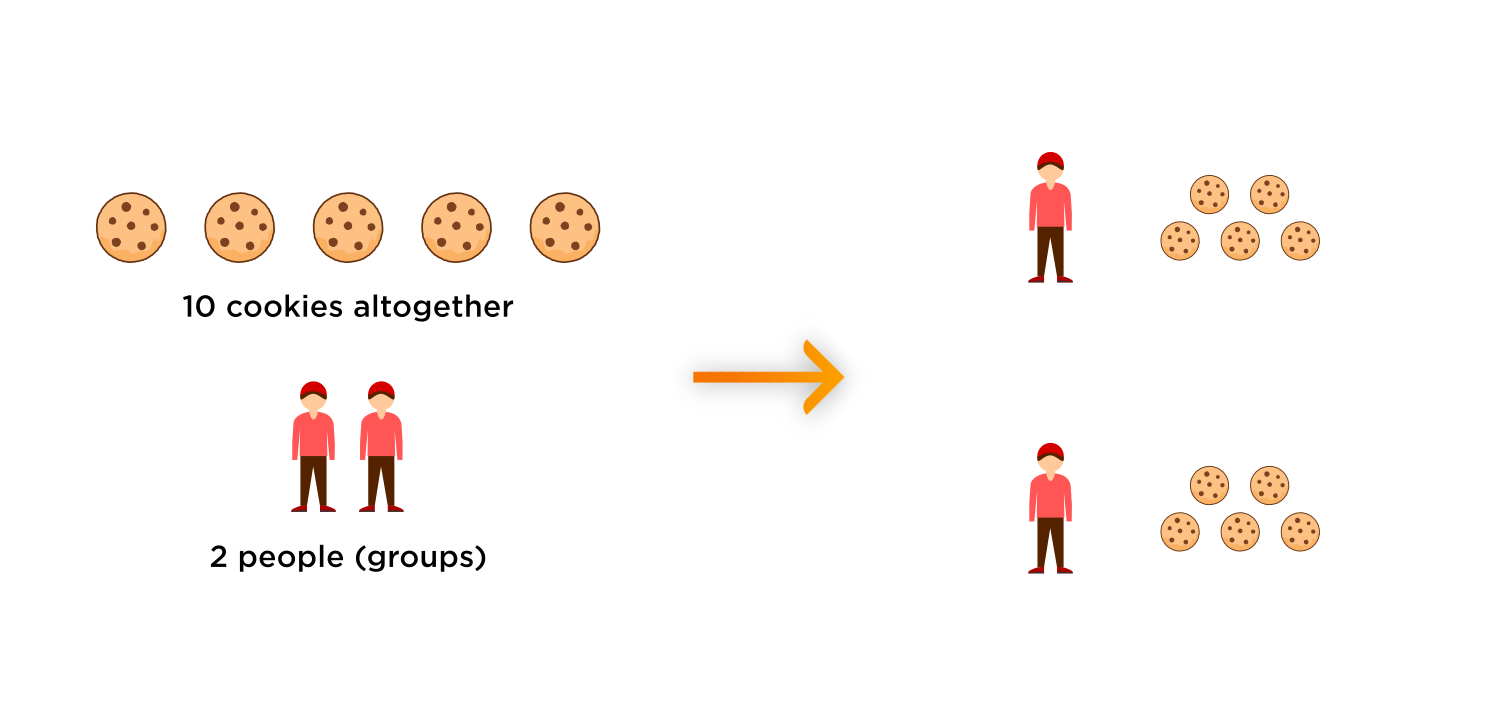
$$ \frac{\textcolor{purple}{10 \text{ altogether } }}{\textcolor{blue}{2 \text{ groups } } } = \textcolor{green}{5 \text{ in each group}} $$
For example, we could be sharing \( \textcolor{purple}{10}\) cookies with \( \textcolor{blue}{ 2}\) people. Each person gets \( \textcolor{green}{ 5}\) cookies.
Going back to the original problem, we want to find the decimal representation of \(\frac{1}{3}.\) In other words, we want to find out \( \textcolor{green}{\text{ how much cookie each person gets } }\) if we are sharing \( \textcolor{purple}{1}\) cookie with \( \textcolor{blue}{ 3}\) people.
$$ \frac{\textcolor{purple}{1 \text{ altogether } }}{\textcolor{blue}{3 \text{ groups } } } = \textcolor{green}{? \text{ in each group}} $$
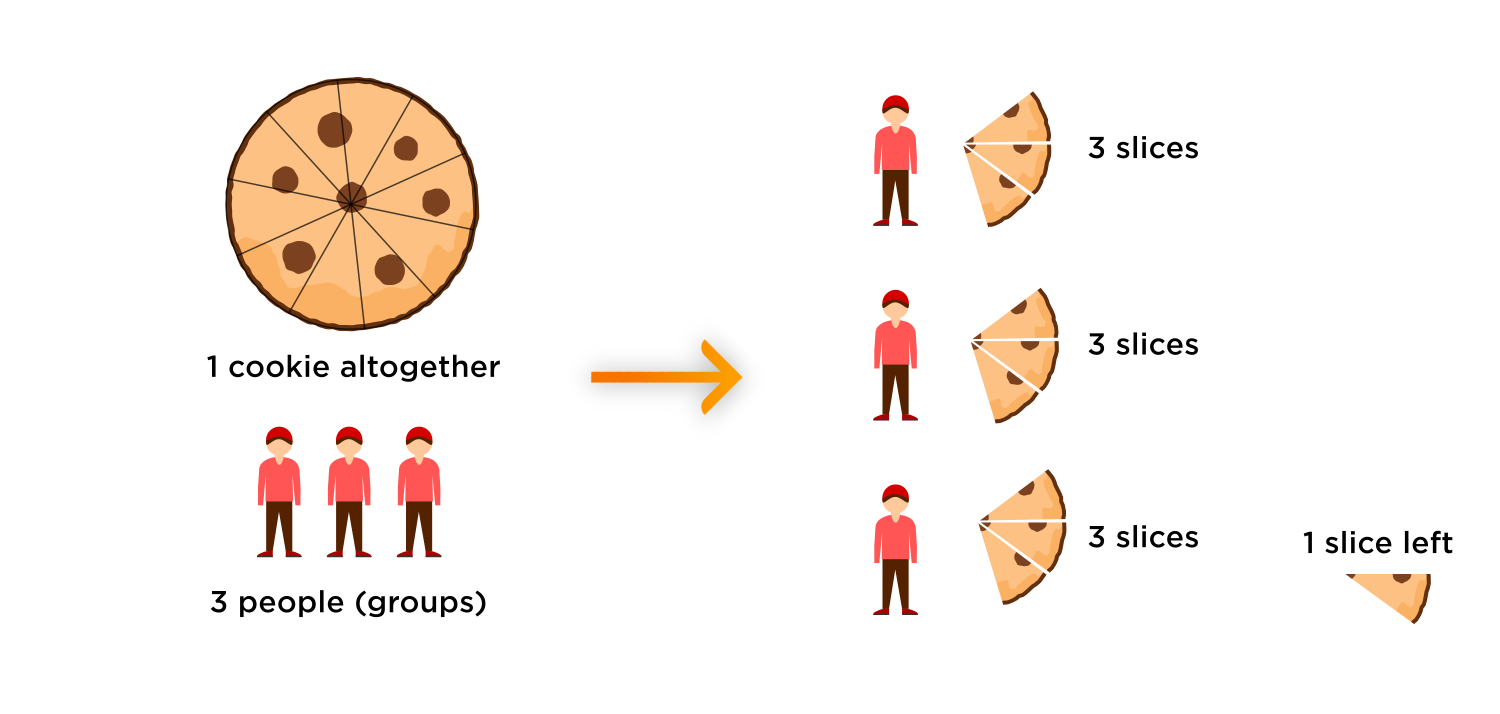
Each person gets \(3\) slices, and there is one slice left.
That one slice equals \(10\) slivers, so we can now share the \(10\) slivers over the \(3\) people.
Each person gets \(3\) slivers, and there is one sliver left.
That one sliver equals \(10\) hairs, so we can now share the \(10\) hairs over the \(3\) people.
Each person gets \(3\) hairs, and there is one hair left.
And on, and on, and on...
To summarize, each person gets \(3\) slices, \(3\) slivers, and \(3\) hairs, and the pattern continues with a never-ending sequence of \(3\)'s.
$$ \boxed{ \frac{1}{3} = 0.\overline{333}\ldots } $$
