Week 3 challenge general question: I don't get those subscript questions

The Blade Dancer

Module 3 Week 3 Day 10 Challenge Part 3 Explanation

What it mean when it says there are certain subsets of a set, like (1, 2, 3, 4, 5)? Also, what is the question asking for when it's something like:

When G subscript 1 is 1, and G subscript 2 is 2,

and so G subscript n = G subscript n-1 + G subscript n-2,

what is G subscript 5?

(I don't know how to type subscript lol)

I don't get those subscript questions because the question feels like it's inconsistent and because I just don't know what it means. Can you explain how to solve those questions or a link to a video that talks about it? Thanks.

The Blade Dancer

Also if G subscript 1 is G subscript n-1 or something like that then how do we calculate G subscript n-1? Again, link or explanation please. Thanks in advance.

debbie

@The-Blade-Dancer This is a good question! (And by the way, you can type the subscript by typing this:

\\( G_1 \\)

which gives you $ G_1$

or, for a multi-digit subscript, you can type this:

\\( G_{n-1} \\)

which gives you $ G_{n-1}.$ )

In general, a variable with a subscript of $n$ refers to the $n^{\text{th}}$ term of a sequence. It doesn't matter what the sequence is. It doesn't have to be an arithmetic (e.g. $3, 6, 9, 12, 15, 18, \ldots $ ) sequence or a geometric (e.g. $5, 25, 125, 625, \ldots $) sequence. A sequence is merely a set of numbers whose terms are dictated by a set of rules.

For example, I could have this sequence consisting of the positive square numbers, called $S$:

$$ S = 1, 4, 9, 16, 25, 36, 49, 64, 81, \ldots $$

Here $S_5 = 25,$ since the $5^{\text{th}}$ square number is equal to $25.$

The pattern that governs a sequence can vary; it just must be consistent over all terms. Consider the sequence, $O,$ whose $n^{\text{th}}$ term consists of $n$ zeroes sandwiched between two ones, like this:

$$ O = 101, 1001, 10001, 100001, \ldots $$

In this case, $O_4 = 100001,$ since the $4^{\text{th}}$ term is $100001.$

This sequence, called $F,$ consists of fractions of the form $ \frac{1}{n}.$

$$ F = \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \ldots $$

Here, $F_2 = \frac{1}{2}.$

We can even have non-mathematical sequences! Let $H$ be the sequence of Harry Potter book titles.

$$\begin{aligned} H_1 &= \text{ Harry Potter and the Sorcerer's Stone} \\ H_2 &= \text{ Harry Potter and the Chamber of Secrets}\\ H_3 &= \text{ Harry Potter and the Prisoner of Azkaban} \\ H_4 &= \text{ Harry Potter and the Goblet of Fire} \\ H_5 &= \text{ Harry Potter and the Order of the Phoenix} \\ H_6 &= \text{ Harry Potter and the Half-Blood Prince} \\ H_7 &= \text{ Harry Potter and the Deathly Hallows} \\ \ldots \end{aligned} $$

In Module 3, we looked at a special type of sequence called a recursive sequence. The interpretation of a term like $a_n,$ which we encountered in the Day 10 tiling lesson, is that it equals the $\textcolor{blue}{\text{ number of ways to construct an object of length or size } n}.$ This is a bit different from the sequences we just saw, but it still counts as a sequence.

$$\begin{aligned} a_1 &= \text{ number of ways to construct something of length } 1 \\ a_2 &= \text{ number of ways to construct something of length } 2\\ a_3 &= \text{ number of ways to construct something of length } 3 \\ a_4 &= \text{ number of ways to construct something of length } 4\\ a_5 &= \text{ number of ways to construct something of length } 5\\ a_6 &= \text{ number of ways to construct something of length } 6\\ a_7 &= \text{ number of ways to construct something of length } 7\\ \ldots \end{aligned} $$

So, why was it often the case that $G_1 = 1,$ for some recursive sequence, $G?$ It's because there aren't many ways to make something of length $1.$ In the case of tiling, where there were only $1 \times 1$ squares and $1 \times 2$ rectangles that we could use, we could only use the square, so there was only one way.

In fact, you asked about how to calculate $G_{n-1},$ and this relates very much to how and why we start by calculating $G_1.$ You see, it's much easier to visualize the ways to make something if the something is very small. It's very easy to figure out $G_1$ and $G_2$ by hand. It's just the terms later on, like $G_{10} (\text{ the number of ways to make something of length } 10 ),$ which are very difficult to picture in your head.

This is where recursion comes to the rescue!

The idea is that you can figure out how to take one step; you know how to make your thing one unit of length longer. You know how to grow the sequence. This means that if someone supplies you with all the ways to make a sequence of length $9,$ you will be able to figure out all the different sequences of length $10.$ Never mind that we don't really know how many sequences of length $9$ there are yet; we can worry about that later! First concentrate on how to grow a given sequence.

And don't forget that the values of the $a_n, G_n,$ or whatever term you are referring to in the sequence, equal the $\text{ number of ways to make a sequence of length } n.$

In the Day 10 Challenge lesson, we were able to grow our tile strip by adding either a $1 \times 1$ square or a $1 \times 2$ rectangle to the end.

We could get a $1 \times 3 $ length strip by adding a square to a $1 \times 2$ strip or adding a rectangle to a $1 \times 1$ length strip.

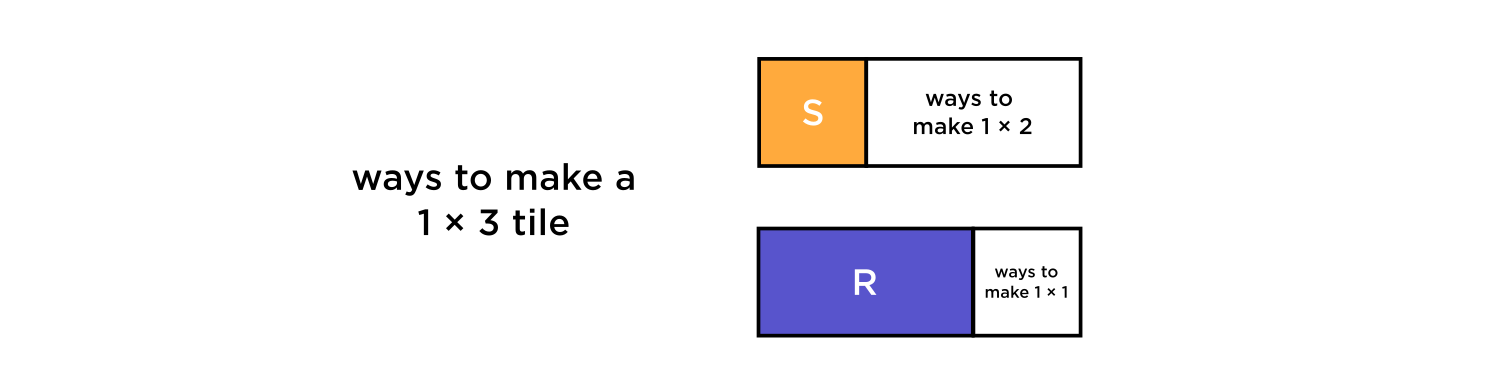
Thus

$ \# \text{ ways to make a strip of length } 3 = \# \text{ ways to make a strip of length } 2 + \# \text{ ways to make a strip of length } 1.$

Using math notation, this is written as

$$ a_3 = a_2 + a_1 $$

Moving on, we can do this for the next term in the sequence, $a_4.$ We can make a $1 \times 4 $ length strip by adding a square to a $1 \times 3$ strip or adding a rectangle to a $1 \times 2$ length strip.

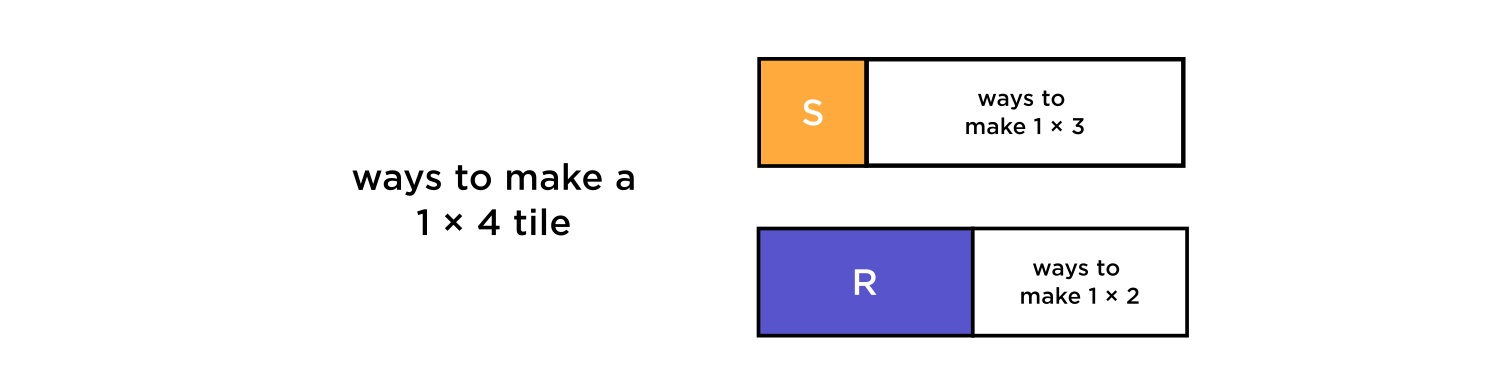
Thus

$ \# \text{ ways to make a strip of length } 4 = \# \text{ ways to make a strip of length } 3 + \# \text{ ways to make a strip of length } 2.$

Using math notation, this is written as

$$ a_4 = a_3 + a_2 $$

We can keep going: for the next term in the sequence, $a_5,$ we can make a $1 \times 5 $ length strip by adding a square to a $1 \times 4$ strip or adding a rectangle to a $1 \times 3$ length strip.

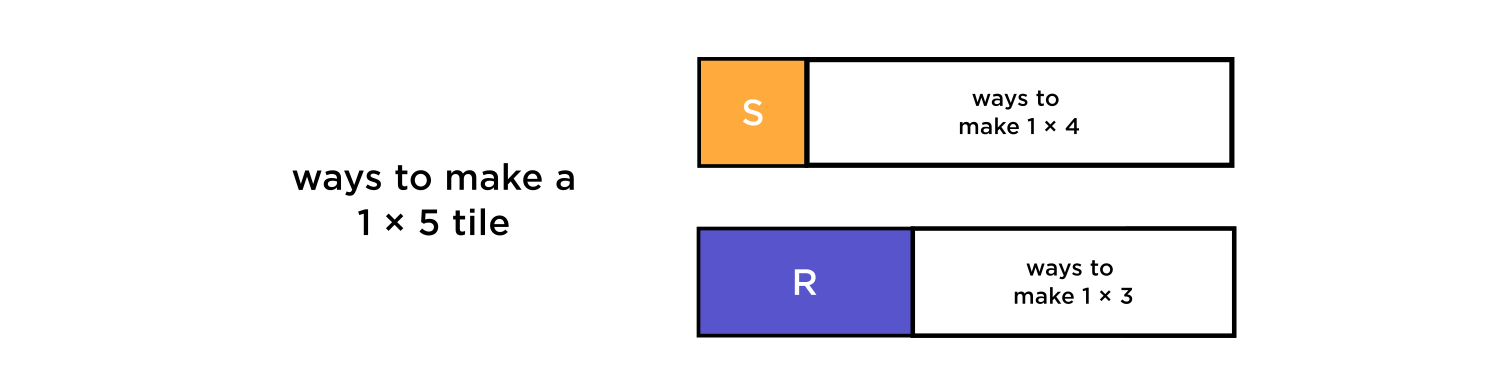
Thus

$ \# \text{ ways to make a strip of length } 5 = \# \text{ ways to make a strip of length } 4 + \# \text{ ways to make a strip of length } 3.$

Using math notation, this is written as

$$ a_5 = a_4 + a_3 $$

We can illustrate the $n=5$ case below, by drawing out all the ways to create an $n=3$ strip (there are 3 ways) and all the ways to create an $n=4 $ strip (there are 5 ways).

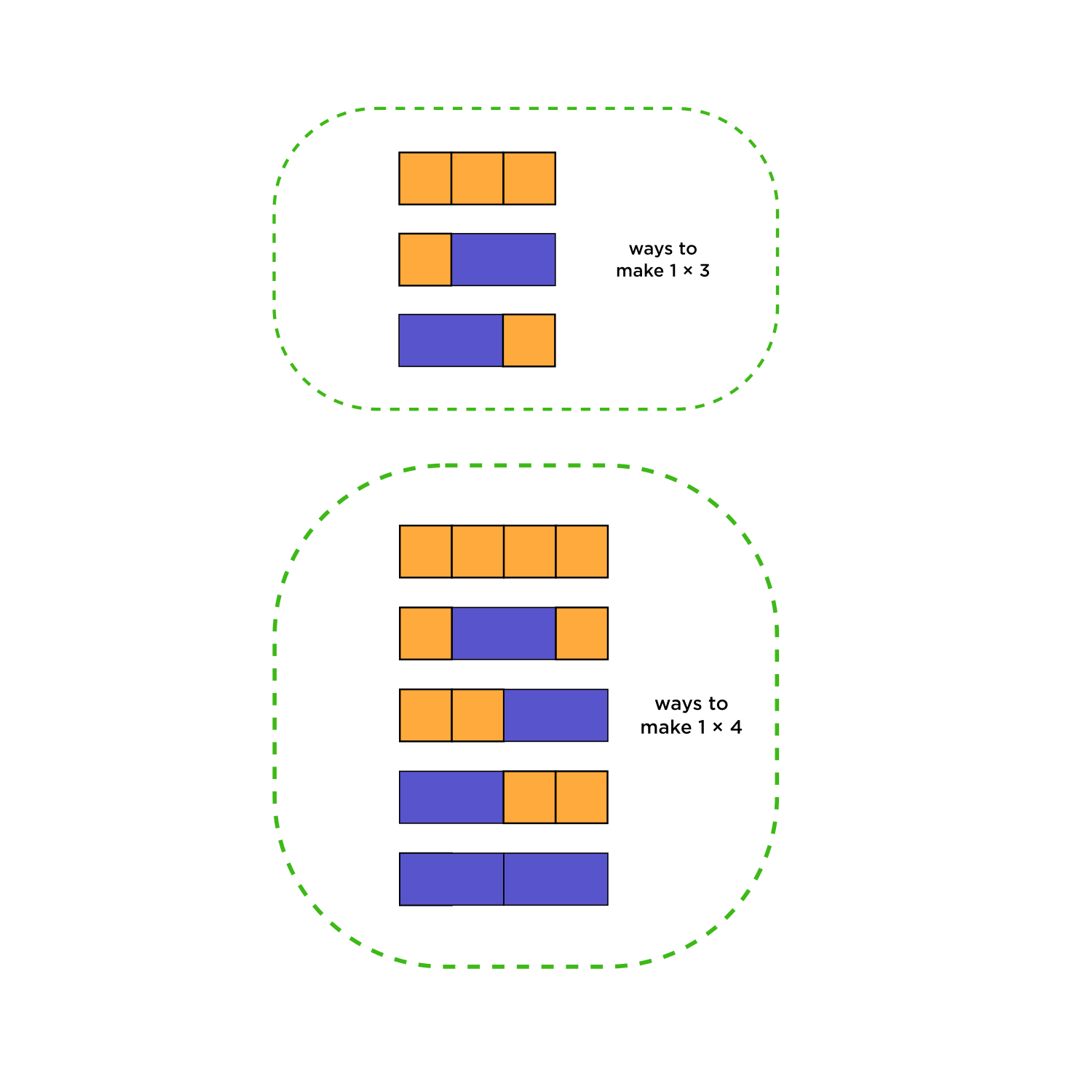
Now, to make an $n=5$ strip, we can either add a square to an $n=3$ strip or add a $1 \times 2$ rectangle to an $n=4$ strip.

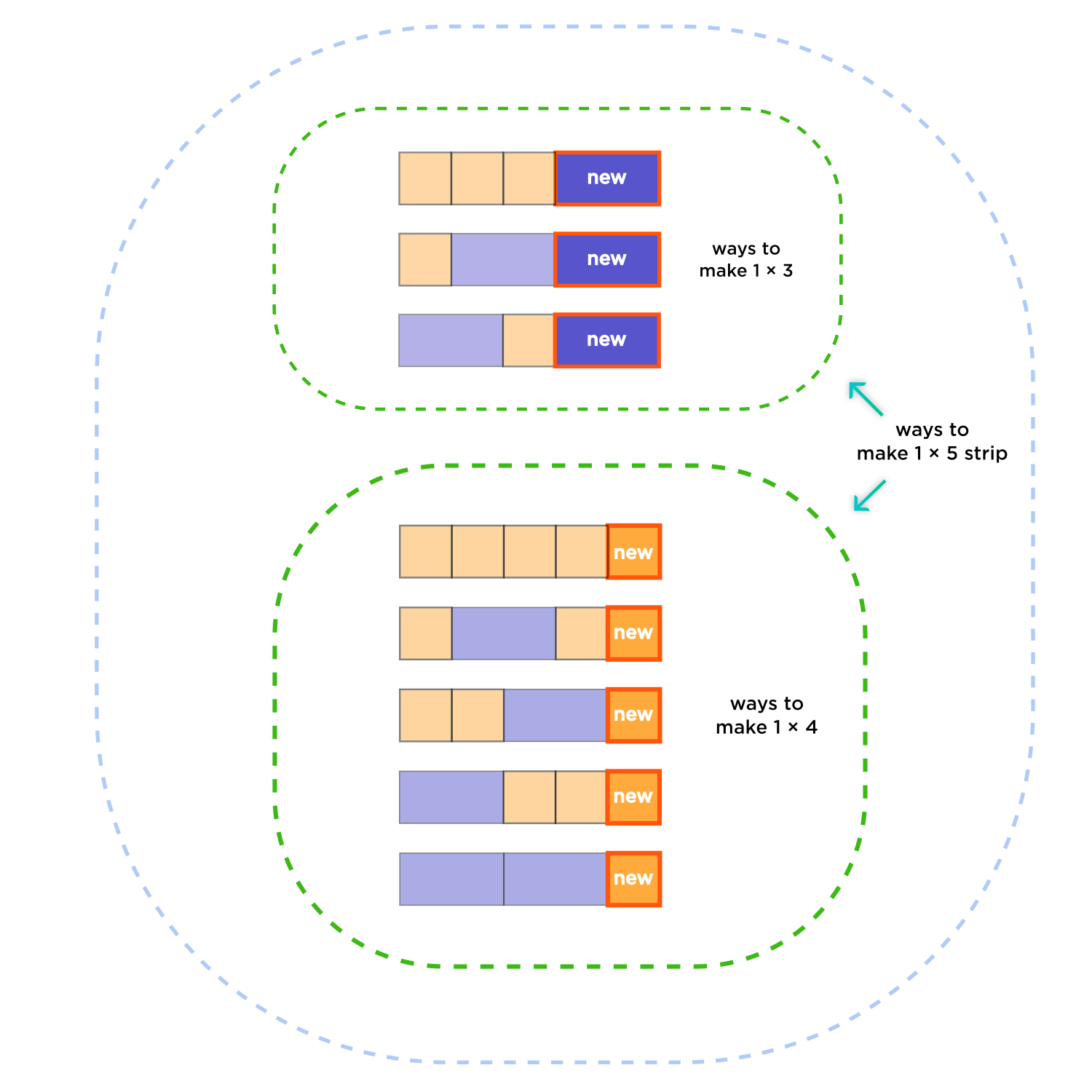
Thus to find the number of ways to get an $n=5$ length strip, you just add the ways to make an $n=4$ length strip and the ways to make an $n=3$ length strip.

$$ 3 \text{ ways to make a 3-length strip} + 5 \text{ ways to make a 4-length strip} = 8 \text{ ways to make a 5-length strip} $$

$$ 3 + 5 = 8 $$

The number $8$ happens to be the sixth Fibonacci number, and this general recursion formula for the Fibonacci sequence, $a_n = a_{n-1} + a_{n-2},$ happens to be the same as the formula for finding the solution to this question of how many ways there are to tile an $n$-length strip with just $1 \times 1$ squares and $1 \times 2$ rectangles. It's neat how there are so many connections in math that draw seemingly different concepts together, but the connection between Fibonacci, recursion and the number of ways to tile something is truly astonishing and is a marvel of mathematics!

Here are some links to videos or posts reviewing these topics:

Module 3 Week 3 Day 10 Challenge Lesson, Tiling Strips

Forum Post: Module 3 Week 3 Day 10 Challenge Part 3, Tiling Recursion

Module 3 Week 3 Day 10 Your Turn Part 1 Lesson: Tiling Rectangles (see the mini-question explanation)

Module 3 Week 3 Day 11 Challenge Lesson, Beads on a Line, With Constraints

Module 3 Week 3 Day 11 Your Turn Lesson, Beads on a Line

Forum Post: Module 3 Week 3 Day 10 Your Turn Part 4, "Does That Recursion Have Anything To Do With Fibonacci?"

The Blade Dancer

Godsend, very helpful, thanks a lot.

RZ923

@debbie said in Week 3 challenge general question: I don't get those subscript questions:

$$\begin{aligned} H_1 &= \text{ Harry Potter and the Sorcerer's Stone} \\ H_2 &= \text{ Harry Potter and the Chamber of Secrets}\\ H_3 &= \text{ Harry Potter and the Prisoner of Azkaban} \\ H_4 &= \text{ Harry Potter and the Goblet of Fire} \\ H_5 &= \text{ Harry Potter and the Order of the Phoenix} \\ H_6 &= \text{ Harry Potter and the Half-Blood Prince} \\ H_7 &= \text{ Harry Potter and the Deathly Hallows} \\ \ldots \end{aligned} $$

$H_8 = \text{Harry Potter and the Cursed Child}$
$H_9 = \text{Harry Potter and the Non-Existent Book}$

divinedolphin

@RZ923 Cursed child is a play, and it isn't the Non-Existent Book, its another invisible book. Remember when Flourish and Blotts bought all those copies of The Invisible Book of Invisibility? Only for this book, almost all the bookstores in the world bought copies, and they all disappeared!