Ok I was understanding this but what do powers of base 10 have to do with anything?
-
Module 3 Week 2 Day 7 Your Turn Part 2
Ok I was understanding this but what do powers of base 10 have to do with anything?
-
@The-Blade-Dancer That's a good question; here Prof. Loh is writing \(11\) as \(10 + 1.\) We want
$$ 11 \times 11 \times 11 \times 11 \times 11 \times 11 $$
which is the same as
$$ (10 + 1) ( 10 + 1) ( 10 + 1) (10 + 1) (10 + 1) (10 + 1). $$
This will give us terms consisting of integers multiplied to powers of \(10\) ranging from \(10^0\) to \(10^6,\) and we know that multiplying a number by a power of \(10\) "shifts" it in the place value column. For example, multiplying \(3\) by \(10^4\) "shifts" the \(3\) over by four spots, from the ones column to the ten thousands column.
$$ 3 \rightarrow 3 \times 10^4 \\ 3 \rightarrow 30,000 $$Now the trick is that the integers multiplied to the power of \(10\) can be found in a special way: by using Pascal's Triangle!
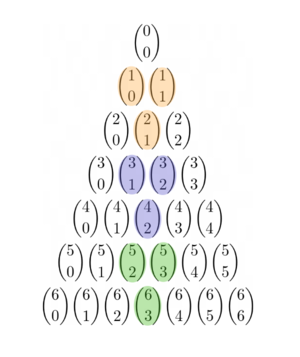

For the Binomial Theorem that Prof. Loh showed us tells us what the coefficients of the expansion of \((x+1)^6\) are:
$$(x + 1)^6 = \binom{6}{0} x^6 1^0 + \binom{6}{1} x^5 1^1 + \binom{6}{2}x^4 1^2 + \binom{6}{3}x^3 1^3 + \binom{6}{4}x^2 1^4 + \binom{6}{5}x^1 1^5 + \binom{6}{6} x^0 1^6 $$These Binomial Coefficients, \( \binom{6}{0}, \binom{6}{1}, \binom{6}{2}, \binom{6}{3}, \binom{6}{4}, \binom{6}{5}, \binom{6}{6},\) happen to be the values of the 7th row of Pascal's Triangle, and the beautiful thing is that since these Binomial Coefficients are multiplied to successive powers of \(10,\) we can simply write the result of \( 11^6 \) by writing \( \binom{6}{0},\) then shifting our pen to the left, then writing \(\binom{6}{1},\) then shifting our pen to the left, then writing \(\binom{6}{2},\) etc. etc. You could say that these binomial coefficients don't "overlap" each other in our large addition.
$$\begin{aligned} 1 & \\ 6 \text{ } & \\ 15 \text{ } & \\ 20 \text{ } \text{ } \text{ } & \\ 15 \text{ } \text{ } \text{ }\text{ } \text{ } & \\ 6 \text{ } \text{ } \text{ }\text{ } \text{ } \text{ } \text{ } & \\ 1 \text{ } \text{ } \text{ }\text{ } \text{ } \text{ } \text{ } \text{ } \text{ } & \\ \end{aligned} $$If you add these up, you get the answer, \(1771561!\)
