What does the 5 have to do with the 3 choose 3 mentioned in the mini question?
-
Module 3 Week 2 Day 6 Your Turn Part 1 Mini-Question

What does the 5 have to do with the 3 choose 3 mentioned in the mini question?
-
This is a little hard to explain with words, so let's look at some pictures and try to properly understand exactly what's going on here. I'm going to borrow Professor Loh's graphics once again:
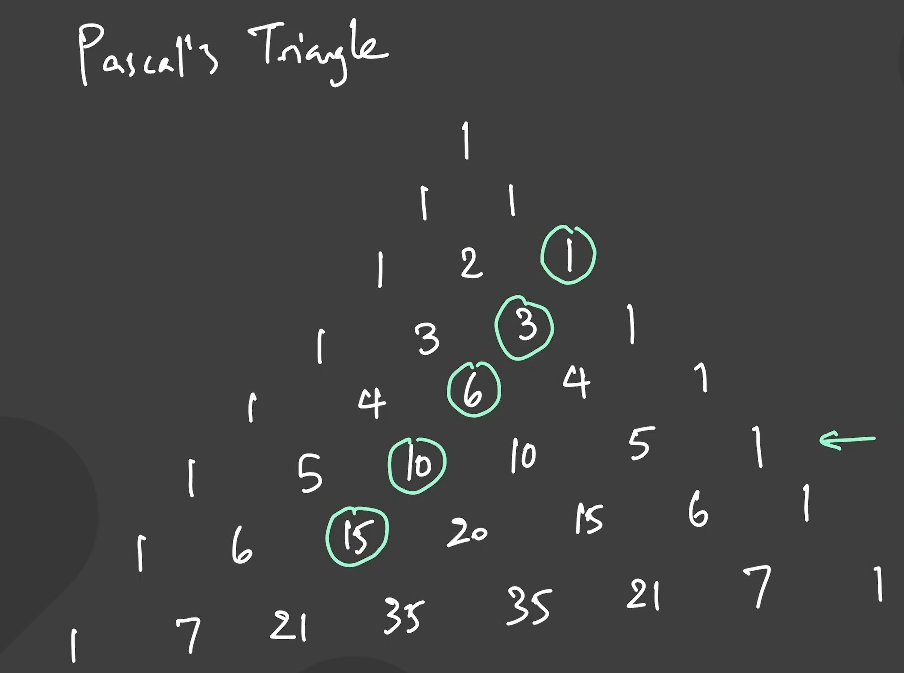
The basic idea of Pascal's Triangle is that any number is the sum of the two numbers to the right and left in the row above it. How can we use that to our advantage if we want to compute the sum of a diagonal quickly?
As Professor Loh states in the video, we use something called the Hockey Stick Identity. At the heart of it is the concept of a partial sum. Instead of instantly summing \( 1 + 3 + 6 + 10 + 15 \), we can sum \( 1 + 3 = 4 \) first, and then add the rest later. In this way, we can "baby step" our way through our full sum, and use Pascal's triangle to make our life easier.
Let's turn back to our image, for a second.
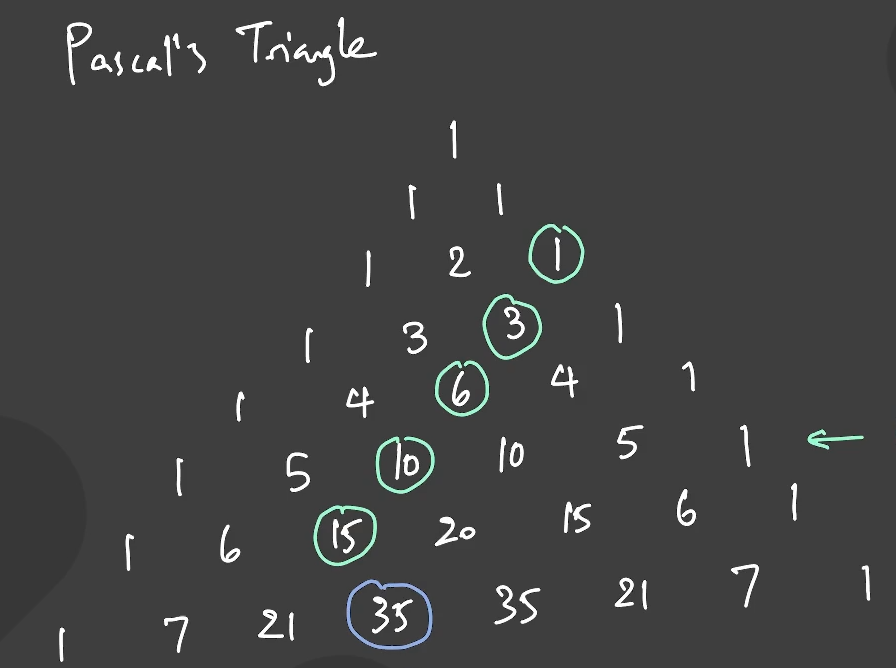
How does this idea of a partial sum help us compute our overall sum? Well, at each step of the process, starting with the smallest numbers on our list, the partial sum of the numbers you've added so far is found down and to the right. $$1 + 3 = 4$$
$$1 + 3 + 6 = 4 + 6 = 10$$
$$1 + 3 + 6 + 10 = 4 + 6 + 10 = 10 + 10 = 20$$ and so on.At each stage, we're relying on the fact that our earlier partial sums are correct. However, it's not quite correct to say that our first partial sum is \(1 + 3 = 4\). What if we rewrite our sum as \(0+ 1 + 3 + 6 + 10 + 15 \)? Then our first partial sum is \(0+1 = 1\)! And sure enough, below and to the right of our 1, we find another 1. Now let's look at the question:

Our sum here, rewritten as above, is \(0 + 4 + 10 + 20\). But \( 0 + 4 \neq 5\)! We have a problem here. Since our very first partial sum is off by 1, the later ones will be off by 1 as well!
So in short: for the Hockey Stick Identity to work properly, the first number we're summing must be equal to the number below and to the right of it. This only happens at the edge of Pascal's Triangle, so the Hockey Stick Identity can only be used along diagonals where the numbers reach all the way to the edge.
Can you think of a way to adapt the Hockey Stick Identity so it's usable on any diagonal?