This doesn't make sense...
-

Shouldn't it be marked out that it's everything minus 5 choose 2 because just 5 choose 2 is not equal to 5 choose 3?Also the entire explanation doesn't make sense help what is Prof. Loh trying to do here?
-
Oh wait 5 choose 3 is equal to 5 choose 2 I just found out weird...
-
@The-Blade-Dancer It's great that you noticed this!
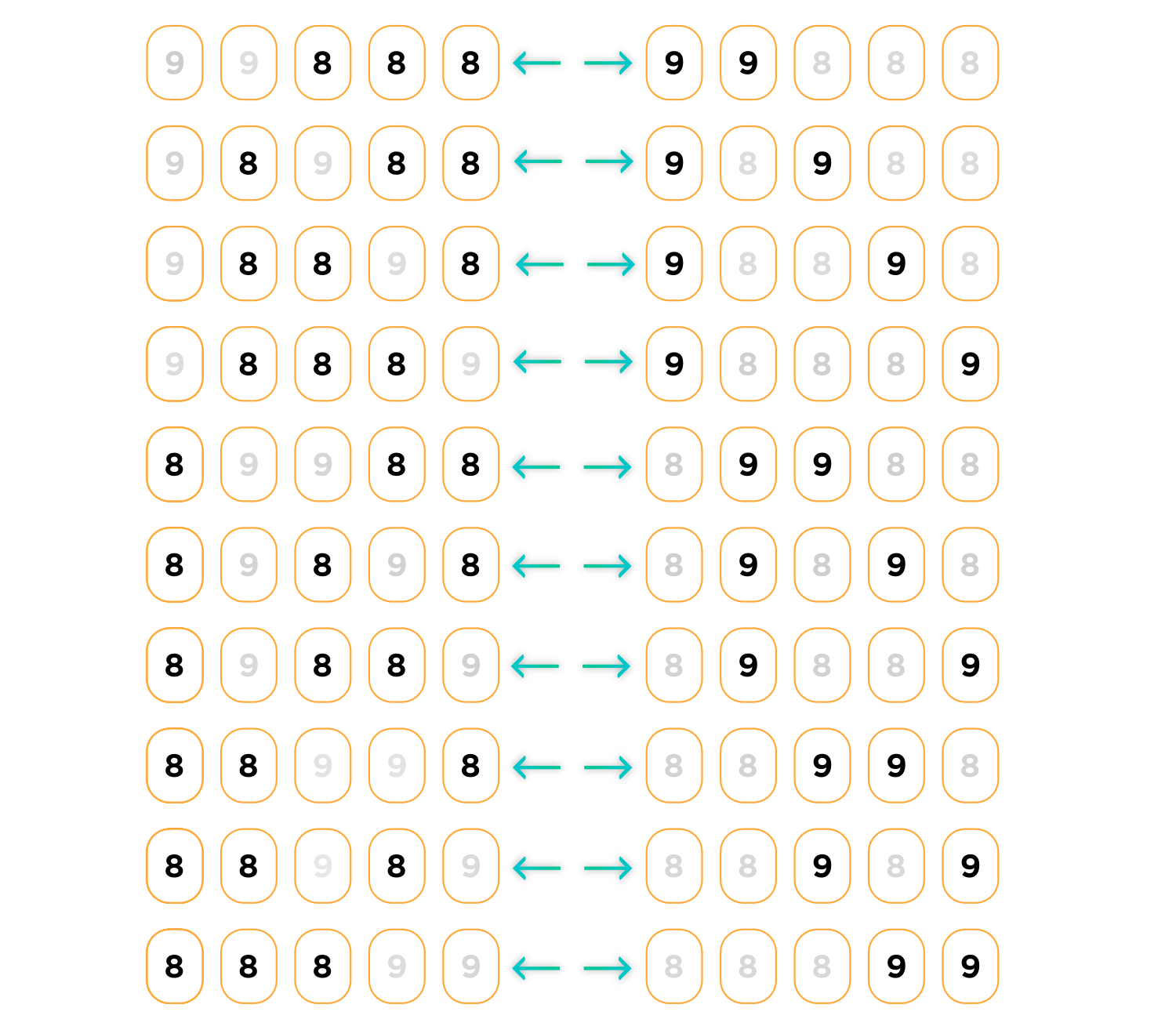
 Yes, you can see from the diagram below that for every way there is to choose two spots, it's equivalent to a way that chooses three spots (the three spots that you don't take).
Yes, you can see from the diagram below that for every way there is to choose two spots, it's equivalent to a way that chooses three spots (the three spots that you don't take).
There are \(10\) ways, and both \(\binom{5}{3} \) and \(\binom{5}{2} \) equal \(10.\)
This is such a cool concept, and you'll see later on in this course the magical symmetry of Pascal's Triangle that lies beneath this general fact that \( \binom{n}{m} = \binom{n}{n-m}.\)
-
@debbie
It's like choosing 3 children to go to a maths competition out of 5 is the same as choosing 2 children to not go to the maths competition out of the same 5. -
@RZ923 Yes!!! That's right!!!!





-
@rz923 Yes, that seems logical