Why is the ratio of △PCD to △PAB the square of the ratio of their sides?
-
Module 2 Week 2 Day 5 Challenge Part 2
Why is ratio of the area of triangle PCD to triangle PAB the square of the ratio of its sides?
-
Hi tidyboar,
Good question! This is actually part of a general result in geometry: If I have two shapes that are similar (so that one is just a scaled-up version of the other), and the "scale factor" is \(r\), then the ratio between their areas is \(r^2\). Here is a picture with some examples:
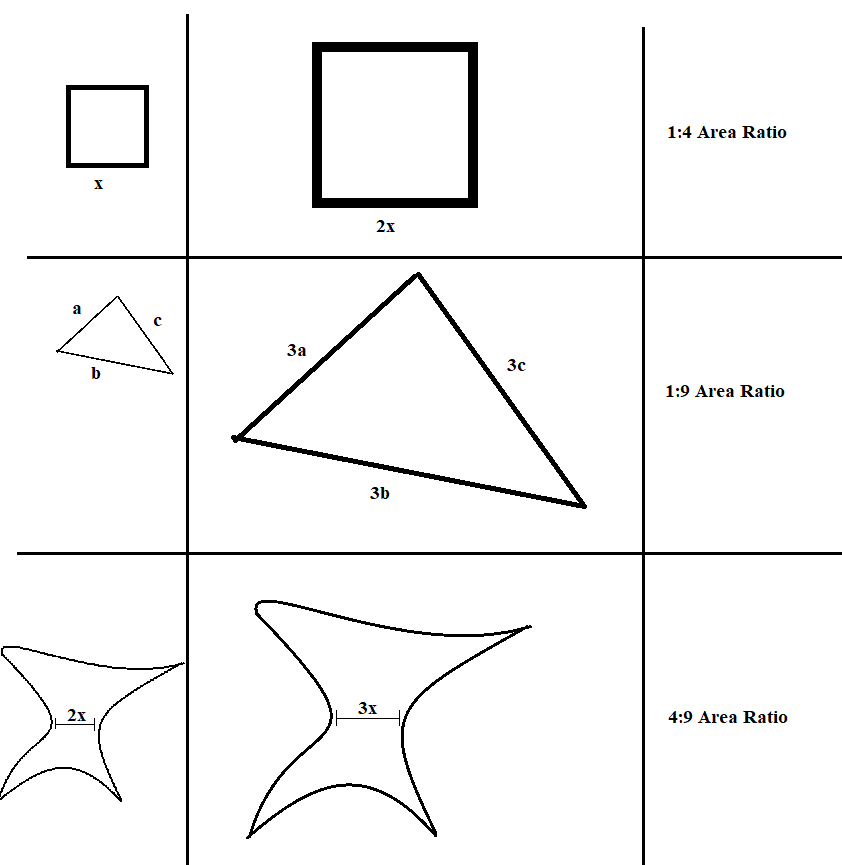
As you can see, it's even true when the shape looks really weird!
To explain why this is true, I think it's best to think about the square example. For squares, it's pretty easy: If the first square has side length \(a\), and the second square has side length \(ar\) (so it's \(r\) times bigger), then their areas are \(a^2\) and \(a^2r^2\), the ratio between the areas will be \(a^2:a^2r^2\), which is just \(1:r^2\)!
So what about a triangle? What if the sides of one triangle are \(a,b,c\), and the sides of the scaled-up triangle are \(ar,br,cr\)?
The key idea is that when you scale-up a triangle, then everything inside the triangle is scaled up by the same factor. So, let's say the base of the triangle is \(b\) and the height is \(h\). Then, the base of the scaled-up triangle must be \(br\), and the height must be \(hr\):
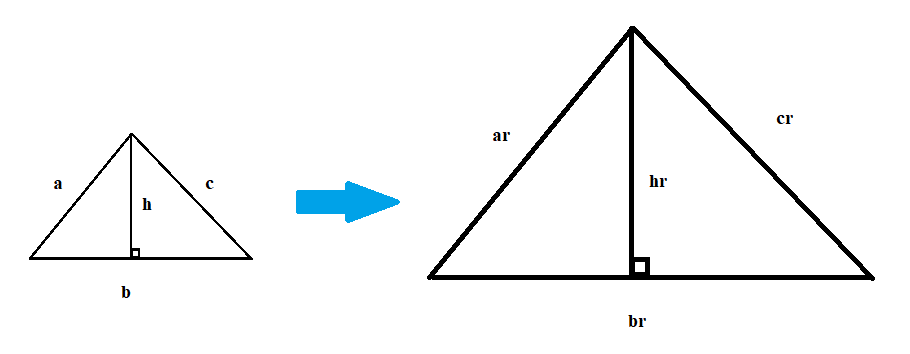
What's the area ratio now? Well, the first triangle has area \(\frac12bh\), and the second triangle has area \(\frac12(br)(hr)=\frac12bhr^2\). That means that the ratio between their two areas is \(\frac12bh:\frac12bhr^2\), which is the same ratio as \(1:r^2\). Ta-da!
You're probably wondering how you can prove this for all possible shapes. It's an interesting question to think about! See if you can come up with any good explanation as to why it would work for every shape you could draw.
Now, to finally answer the original question, we know that the triangles \(\triangle PCD\) and \(\triangle PAD\) are similar, and the ratio of their sides is \(9:15\). That means that \(\triangle PAD\) is \(\frac{15}{9}\) times bigger, or \(\frac{5}{3}\). So, by what we discussed, its area must be \(\frac{25}{9}\) bigger, and that's why the ratio of the areas is \(9:25\).
So in general, if you have two similar triangles with corresponding sides of ratio \(a:b\), then the ratio between the areas will be \(a^2:b^2\).
I hoped that helped. Be sure to let us know if you have more questions. Happy learning!
Thomas
-
@thomas That's amazing, really. Even for the weird stars, the ratio works.

-
This post is deleted! -
Tysm!

-
a little off topic but how would u find the area of that weird star
-
@gameonx That's a really interesting question! From first glance at that shape, I think it would be difficult because the curves aren't just simple arcs of circles... One way you might be able to figure out the area is with a bit more advanced math. If you imagine the shape on the coordinate axes, and you're given the equation of each of the curves that makes up the figure, then you could use calculus to find the area. (This is because calculus allows you to figure out the areas underneath weird curves) Hope that sort of answered your question haha
-
@gameonx hahaha I would be really impressed if someone solves THAT
-
@victorioussheep that would be like imo problem
find and prove the formula for the area of this figure
insert weird star here