For a full revolution of an angle, why not 840?
-
Module 0 Week 4 Day 13 Challenge Explanation Part 2
Why did people use 360(24 factors) instead of 840(32 factors), which is the 3-digit number with most factors, as the angle of a full revolution?
Thanks
-
360 was a common number back then. The days in a year were estimated to be about 360 days, Babylonians (first mathematicians) had a base-60 system, and 360 is still has quite a lot of factors. Besides, 360 degrees is enough work for me I'd like my math class to be easier :).
https://www.quickanddirtytips.com/education/math/why-does-a-circle-have-360-degrees
-
@The-Darkin-Blade thanks

-
Hi @RZ923!
There are so many different theories. Let me show you one of them - the one that @The-Darkin-Blade mentioned: the base-60 system that the first mathematicians used.
The Sumerians and Babylonians were known to use the Sexagesimal numeral system. The sexagesimal system is one with a base value of 60, whereas the current system we use is known as the decimal system and has a base value of 10. So, once we reach the 10th number, we start repeating the symbols (of previous numbers, from 0 to 9) to form new numbers.
The Babylonians had 60 different symbols with which they formed numbers. Again, why would they use 60? Because 60, just like 360, is a highly composite number with up to 12 factors. Just as we can count 10 on our fingers for the decimal system, we can also count to 60. Start by counting the knuckles of the 4 fingers (not the thumb) on your right hand. 12, right? Now, on the other hand, raise any of those fingers to remember that you finished one iteration and got the number 12. Now, repeat the same procedure as many times as the number of fingers remaining on the left hand. The number you will end up with is \(12 \text{ knuckles} \times 5 \text{ fingers} = 60.\)
If we were to draw an equilateral triangle with side length equal to the radius of a circle and place one vertex of the triangle at the center of the circle, then a total of six such equilateral triangles could fit inside the circle. Since the Babylonians used the sexagesimal numeral system, the total degrees in each triangle was given a base value of 60.
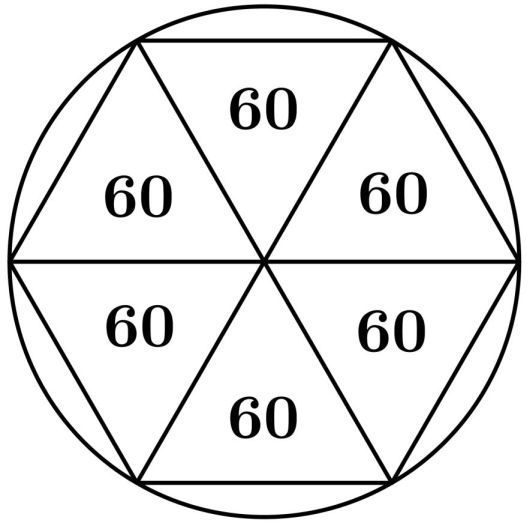
Thus, \(6 \text{ triangles}\times 60 \text{ base value}\) gives us a value of \(360.\) -
@nastya thanks as well
