Why do we scale by 10/ sqrt 2?
-
Module 2 Week 1 Day 2 Challenge Part 3
Sometimes my brain needs a second to recover from this stuff. Why do we scale by 10/ sqrt 2?
-
@The-Darkin-Blade

Luckily, there is another way to find the height of all of these triangles!
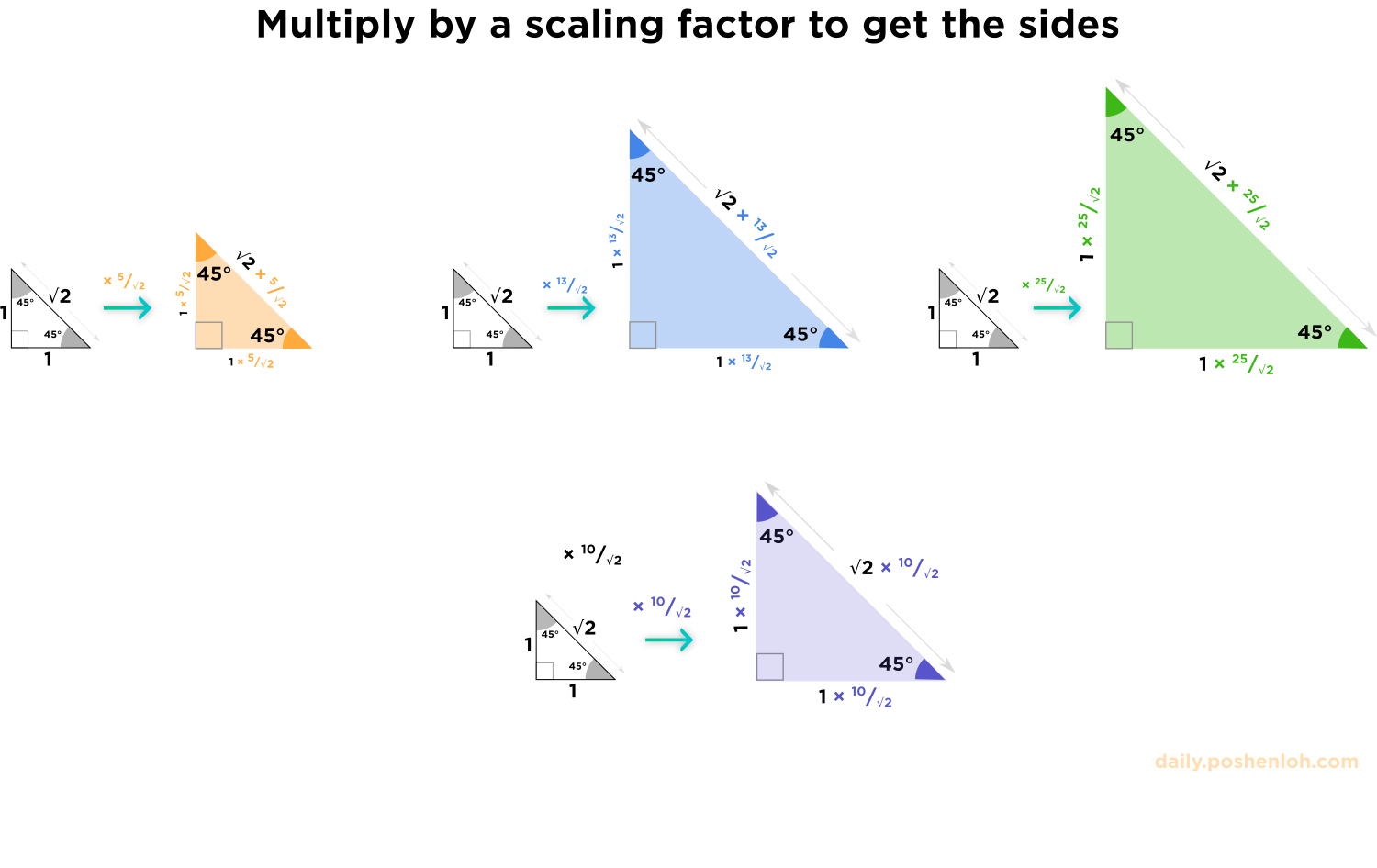
As we know, similar triangles have equal ratios of their sides. So, if we know the sides of one triangle and the scale factor (ratio of sides) of those similar triangles, then we will be able to find the sides of the second triangle by just multiplying the side-lengths of the first one by the scale factor (ratio)!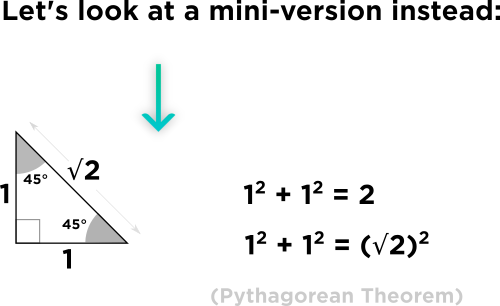
Let's consider a triangle that will be similar to our isosceles right triangles and whose sides are given. One such triangle will be a \(1-1-\sqrt{2}\) right triangle. The ratios of these similar triangles will be:
$$\frac{{\color{orange}\text{\bf{h}}-\text{\bf{h}}-\bf{5}\text{ right triangle}}}{1-1-\sqrt{2}\text{ right triangle}}={\color{orange}\boxed{\frac{5}{\sqrt{2}}}}=\frac{\color{orange}\text{\bf{h}}}{1}=\color{orange}\text{\bf{h}}$$
$$\frac{{\color{blue}\text{\bf{h}}-\text{\bf{h}}-\bf{13}\text{ right triangle}}}{1-1-\sqrt{2}\text{ right triangle}}={\color{blue}\boxed{\frac{13}{\sqrt{2}}}}=\frac{\color{blue}\text{\bf{h}}}{1}=\color{blue}\text{\bf{h}}$$
$$\frac{{\color{green}\text{\bf{h}}-\text{\bf{h}}-\bf{25}\text{ right triangle}}}{1-1-\sqrt{2}\text{ right triangle}}={\color{green}\boxed{\frac{25}{\sqrt{2}}}}=\frac{\color{green}\text{\bf{h}}}{1}=\color{green}\text{\bf{h}}$$
$$\frac{{\color{purple}\text{\bf{h}}-\text{\bf{h}}-\bf{10}\text{ right triangle}}}{1-1-\sqrt{2}\text{ right triangle}}={\color{purple}\boxed{\frac{10}{\sqrt{2}}}}=\frac{\color{purple}\text{\bf{h}}}{1}=\color{purple}\text{\bf{h}}$$So, in order to find \(\color{purple}\text{h}\) we just need to find the scale factor of our triangle and its similar \(1-1-\sqrt{2}\) right triangle.
Scaling is a way to quickly find the sides of any similar triangle, simply using multiplication: