I don't see how the mini explanation has to do with circles; it mentions triangles and rectangles, but not circles.
-
Module 2 Week 4 Day 16 Challenge Part 3 Mini-Question
I don't see how the mini explanation has to do with circles; it mentions triangles and rectangles, but not circles. Also, does Heron's formula work for rectangles and shapes with more sides. If yes, are there any changes we must make to have it work?
-
@The-Darkin-Blade Nice question! Let's take a look back at the original mini-question:

The triangles come from the "quadrilateral which has a circle inscribed within it," mentioned in the question, called a tangential quadrilateral:

Now, if you draw lines from each corner of the quadrilateral to the center of the inscribed circle, you'll see that the quadrilateral is cut into four triangles. This isn't exactly what this question is talking about; you are right! This question is talking about a triangle with a circle inscribed in it, which is analogous:

We're going to try to connect the following concepts that we've encountered so far:
- The area of the triangle in terms of the side lengths (Heron's Formula)
- The area of the triangle in terms of the areas of the three smaller \(\textcolor{purple}{\text{purple}}, \textcolor{green}{\text{green}}, \text{ and } \textcolor{orange}{\text{yellow}}\) triangles.
- The height of each small triangle happens to equal the radius of the circle.
Knowing these, we can get an expression for the radius of the inscribed circle.
The first step is to write the area of the triangle in two ways (here let's call \(a, b,\) and \(c\) the sides of the triangle, and \(r\) the radius of the inscribed circle):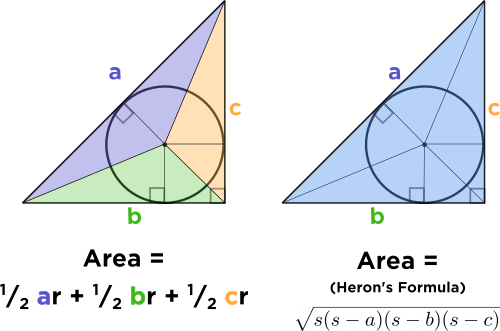
But, look at that! The extremely cool thing is that the expression for the area on the left is really just \(s \times r\)!
So we really have
$$ s \times r = \text{ Heron's formula} $$
and from here we can easily find an expression for the radius of the inscribed circle:
$$ r = \frac{\text{Heron's formula}}{s} $$
$$ = \frac{\sqrt{(s-a)(s-b)(s-c)}}{s} $$Now for the second part of your question! Can we use Heron's Formula for shapes other than triangles? Well, you can't apply the exact formula directly, though apparently there is a similar formula called Brahmagupta's formula, for finding the area of a cyclic quadrilateral. In fact, Heron's Formula is a special case of Brahmagupta's formula. And both Heron's Formula and Brahmagupta's Formula are derived from something called Bretschneider's formula for the area of a quadrilateral. Even more than that, a mathematician found a way to generalize Heron's Formula to pentagons and hexagons. You can read more here to find out!
