What's so special about kites?
-
Module 2 Week 3 Day 12 Challenge Part 3
In this tangential quadrilateral, a quadrilateral which has a circle inscribed inside it, we saw that we can draw four kites inside it.
What's so special about kites anyway, and why does everybody get so so excited when they see a kite?
Let's start by drawing the four tangent points of the tangential quadrilateral, which I've marked here:
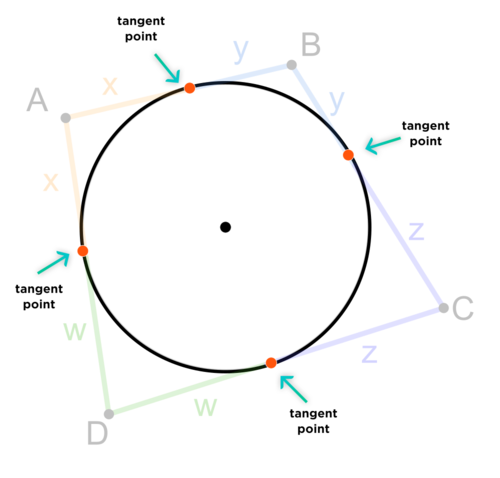
Next we connect these four tangent points to the center of the circle, to get four kites, which I've colored here in four different colors.

So, what's so special about kites?

-
They have two pairs of congruent sides, which you can see in the top left picture. The \(\textcolor{green}{\text{green}}\) sides are the same length, and the \(\textcolor{orange}{\text{yellow}}\) yellow sides are the same length.
-
They have opposite angles which are supplementary; i.e. that add up to 180°, which you can see in the top right picture. Why is this useful? Well, you could perhaps angle chase to find all the angles, and discover that a special angle like 30° or 45° pops out at you. Another reason is....
-
We learned in the Day 8 lesson about cyclic quadrilaterals. For any given quadrilateral, if opposite sides of it are supplementary, then the quadrilateral is cyclic. In other words, it can be inscribed inside a circle. Well, that's what we can do with our kite! Since its opposite angles add up to 180°, we can inscribe it in a circle! This is illustrated in the bottom-right image in the picture above.
Okay, but what can you do with an inscribed quadrilateral? Well, lots of things! You can show that some of the angles are actually the same measure, since they inscribe the same arc of the circle.

The two blue angles have the same measure, since they both inscribe the red arc of the circle.
- The diagonals of a kite intersect at a right angle, as you can see in the picture below.
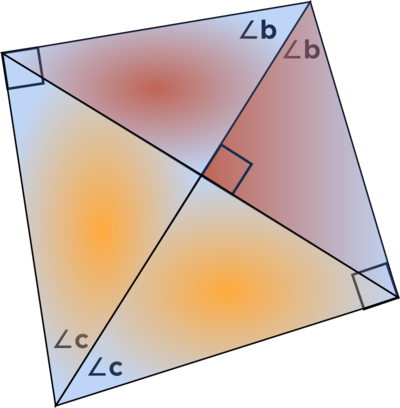
Using the property from 1.), we get two red right triangles that are congruent to each other and two yellow right triangles that are congruent to each other. We know that we can use the Pythagorean Theorem here. But wait! Using the property from 3.), since those two blue angles were the same, we know that the yellow right triangle is similar to the red right triangle!

Not only that, the blue right triangle is also similar to the red and yellow right triangles, so we have every triangle similar to every other triangle! We could use ratios to find the different lengths of the different line segments in this picture. Along with the Pythagorean Theorem, you can find a lot of side lengths with just a tiny bit of initial information.
I hope this shows you why kites are so nice to have around. Whenever you see a kite, you should be really glad!

-