How can I solve this question if the distance between the 2 circles was not given?
-
There was something similar in the weekly challenge. How can I solve this question if the distance between the 2 circles was not given?
-
I don't think you can solve it without the distance between the two circles.
-
The cool trick here is to visualize a large right triangle, \(\bigtriangleup FDE,\) which you can get by sliding the tangent line \(\overline{AB}\) over until it touches the center of the smaller circle:
First, it's helpful to remember that the question states that the circles are \(9\) units apart at their closest point. This is equivalent to the yellow segment highlighted down below.
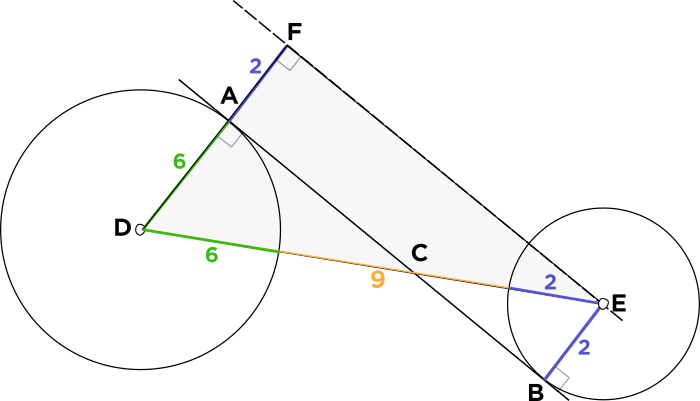
Conveniently, the line connecting the two circles' centers, \(\overline{DE},\) is just this segment of length \(9\) plus the radius of \(6\) and the radius of \(2,\) so this line \(DE = 6 + 9 + 2 = 17.\)
Now we don't even need to know the Pythagorean Theorem, since we know of a right triangle with a leg of \(8\) and a hypotenuse of \(17:\) it's the \(8 - 15 - 17\) right triangle! This means the other leg equal \(15,\) which happens to be the length that we want!