Another way to do "Let's practice"?
-
Module 2 Week 1 Day 3 Challenge Part 4 Mini-Question
I found another way to do the "Let 's practice" question.
We can see by symmetry that the almond is a part of the square with side lengths \(1\). It can be made public two overlapping quarter circles with radius \(1\). The overlapping quarter circles each have an area of \( \pi / 4\), making the total \( \pi / 2\). The square, of course, have an area of \(1\). Minus the square from the two quarter circles and we get \( \pi / 2 - 1\) , same as \( \pi / 4 - 1 / 2\).

-
@RZ923 Wow!!!!! That is so cool! I love this solution; thank you for sharing!



-
@RZ923 said in Another way to do "Let's practice"?:
I found another way to do the "Let 's practice" question.
We can see by symmetry that the almond is a part of the square with side lengths \(1\). It can be made public two overlapping quarter circles with radius \(1\). The overlapping quarter circles each have an area of \( \pi / 4\), making the total \( \pi / 2\). The square, of course, have an area of \(1\). Minus the square from the two quarter circles and we get \( \pi / 2 - 1\) , same as \( \pi / 4 - 1 / 2\).

$$\begin{aligned} \text{ whole almond area } &= 2 \left( \text{ quarter circle areas } \right) - \text{ area of square } \\ &= 2 \left( \frac{1}{4} \pi \right) - 1 \\ &= \frac{1}{2} \pi - 1 \\ \text{ half-almond area } &= \frac{1}{2} \left( \frac{1}{2} \pi - 1 \right) \\ &= \boxed{ \frac{1}{4}\pi - \frac{1}{2} }\\ \end{aligned} $$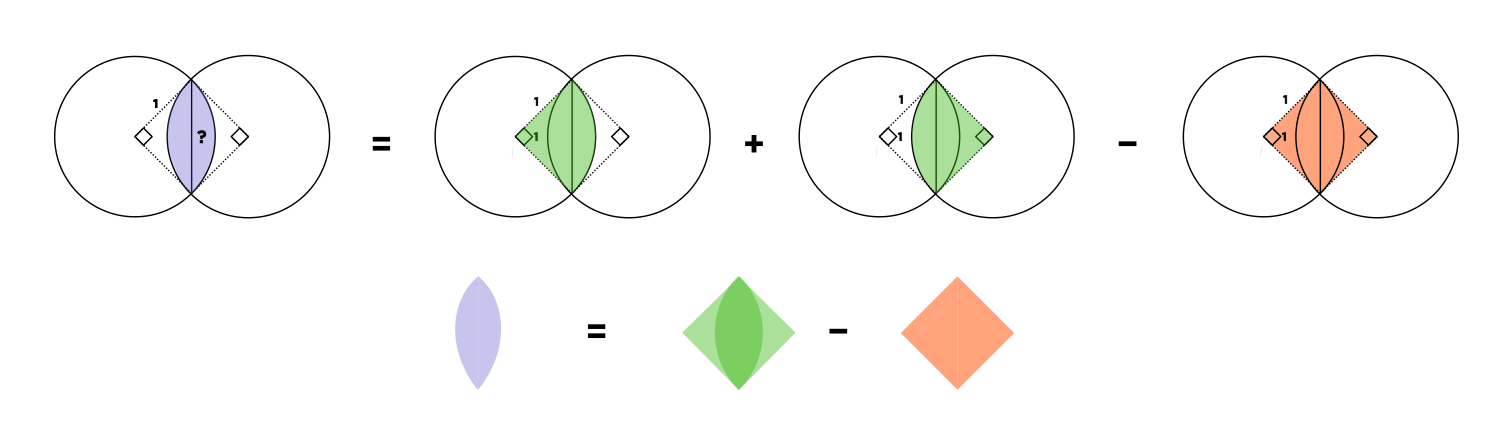
-
@rz923 Cool!
-
OOOOOOOOOOOOOO NOW I KNOW WHAT IT MEANS
took me four months to get back at module 2 and read this lmao