What is 0^0? What is 0 factorial? Please explain why.
-
I know but can you explain 0 factorial?
-
@legendaryboy991 that's why i said i'm not sure
-
@legendaryboy991 is this from module 0?
-
No its just a question in mind
-
0! is 1
this is because there is 1 way to choose nothing
if i had 3! for example it would be 3 ways to choose the first thing, multiplied by 2 ways for the second thing, and then 1 way for the last thing
0! is technically 0 ways to choose the first thing (which is nothing) but there is 1 way to choose nothing
-
@legendaryboy991
0! is equal to 1.
basically, the thought of the operation "factorial" in general is the number of ways to rearrange x amounts of things.
examples:
1!=1=1 way to arrange 1 thing
2!=2x1=2 ways to arrange 2 things
3!=3x2x1=3ways to arrange 3 things
4!=4x3x2x1=24 ways to arrange 4 things
5!=5x4x3x2x1=120 ways to arrange 5 things
6!=6x5x4x3x2x1=720 ways to arrange 6 things
and so on so forth.
When arranging 0 things, you can't multiply something down to 0, so instead, we think about it technicaly-
There's only one way to arrange nothing; by having nothing.
therefore, 0!=1 -
@legendaryboy991 I think 0^0 is undefined because even though n^0 is 1, 0^n is 0.
-
@rz923
tru, although the most common answer is 1, it's still disputed -
@Ashila I just used the calculator and it said 0^0 is 1
-
Btw, like 2! its 2x1 3! is 3x2x1 but 1! is 1x1 but 0! is nothing!
-
@legendaryboy991
The answer of a calculator will display 1 for 0^0, but if you do some digging, the answer is still disputed,
https://www.maa.org/book/export/html/116806
Linked below is an awesome read more about the topic, the basic rundown is, if you're looking at it algebraically,
0^0=1
But if you're doing stuff with limits,
0^0 is an indeterminate form
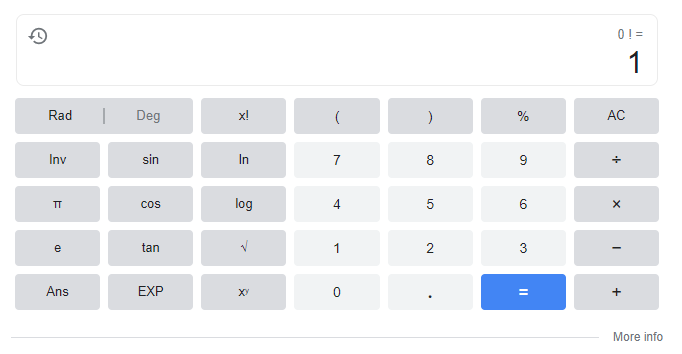
also, I'm not sure what calculator you're using, but the google calculator and my Casio 115 (As well as my Casio 991) give me 0!=1, and 1! isn't nessicarily 1x1, it's just 1, i believe. -
Im using the same and I clicked on that link before
-
its just that what do you multiply in 0! ?
-
like 7! is 7x6x5x4x3x2x1 (you don't need one) is 5040.
-
@legendaryboy991
The thing is, you don't multiply anything in 0!, which is indeed, pretty confusing.
You basically look at it from a logical angle instead;
How many ways are there to arrange 'nothing'?
1.
By having nothing.
So, taking your example, 7! you now have a number of ways to rearrange 7 things,
and 0! would be 1 because there's one way to arrange it.
0! is also what's known as an empty product (Here's a wiki article on empty products:
https://en.wikipedia.org/wiki/Empty_product) -
The thing is how to arrange 0 things????? Suppose you have nothing an you want to arrange it. That makes no sense!
-
@legendaryboy991 it actually sorta does if u think about it-
-
Hey im only going to 4th grade
-
@legendaryboy991 Think of it this way: How many ways to arrange 0 thins? 1: Do nothing. you can't do anything else

It seems that you have started your math journey pretty early!

-