How do we know that any other corresponding sides will multiply by 9/15?
-
Module 2 Day 5 Challenge Part 2
Question is in the title ^
-
@the-blade-dancer Hi again!
 Oh, nice. I think you're referring to the similar triangles \(\bigtriangleup PCD\) and \(\bigtriangleup PAB\) inscribed within the trapezoid below.
Oh, nice. I think you're referring to the similar triangles \(\bigtriangleup PCD\) and \(\bigtriangleup PAB\) inscribed within the trapezoid below.
How do we know that these triangles are similar? Well, \(\angle \textcolor{blue}{PCD}\) and \(\angle \textcolor{blue}{PAB}\) are equal because of the parallel lines \(\overline{CD}\) and \(\overline{AB}\) which are intersected by the transversal \(\overline{AC}.\) The other transversal line, \(\overline{BD},\) which crosses the same parallel lines, creates equal angles \(\angle \textcolor{magenta}{PDC}\) and \(\angle \textcolor{magenta}{PBA}.\) And since \(\angle \textcolor{turquoise}{BPA}\) and \(\angle \textcolor{turquoise}{DPC}\) are formed from the "X" made by \(\overline{BD}\) crossing \(\overline{AC},\) they are also equal. \(\bigtriangleup PCD\) and \(\bigtriangleup PAB\) have the same angles, so they are similar!
It's a little easier to see this if you rotate \(\bigtriangleup PCD\) around so that it's oriented in the same way as \(\bigtriangleup PAB.\)

We can shrink down both triangles by dividing their dimensions by \(15.\) This makes the longest side of \(\bigtriangleup PAB\) only \(1\) long. It's like a reference triangles. Do you see that the longest side of \(\bigtriangleup PCD\) is now \(\frac{9}{15}?\)

Each of the sides of the small triangle are \(\frac{9}{15}\) the length of their corresponding side on the large triangle. (This ratio actually simplifies to \(\frac{3}{5}.\)) To get the ratio of their areas, you square the ratio of their sides. That's just a complicated way of saying the larger triangle has area \(\left( \frac{3}{5} \right)^2\) the area of the smaller triangle.

For more examples about similar triangles, you can read this post by @thomas
 !
!Good luck on the rest of this lesson, and thanks again for asking this question!
@thomas said in Why is the ratio of △PCD to △PAB the square of the ratio of their sides?:
Hi tidyboar,
Good question! This is actually part of a general result in geometry: If I have two shapes that are similar (so that one is just a scaled-up version of the other), and the "scale factor" is \(r\), then the ratio between their areas is \(r^2\). Here is a picture with some examples:
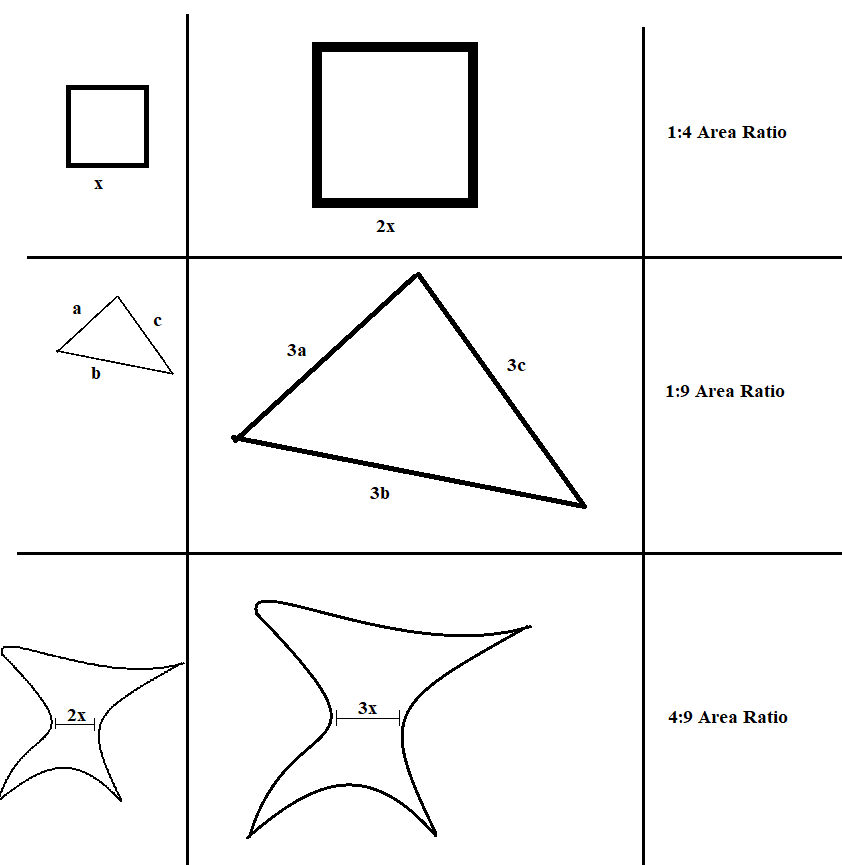
As you can see, it's even true when the shape looks really weird!
To explain why this is true, I think it's best to think about the square example. For squares, it's pretty easy: If the first square has side length \(a\), and the second square has side length \(ar\) (so it's \(r\) times bigger), then their areas are \(a^2\) and \(a^2r^2\), the ratio between the areas will be \(a^2:a^2r^2\), which is just \(1:r^2\)!
So what about a triangle? What if the sides of one triangle are \(a,b,c\), and the sides of the scaled-up triangle are \(ar,br,cr\)?
The key idea is that when you scale-up a triangle, then everything inside the triangle is scaled up by the same factor. So, let's say the base of the triangle is \(b\) and the height is \(h\). Then, the base of the scaled-up triangle must be \(br\), and the height must be \(hr\):
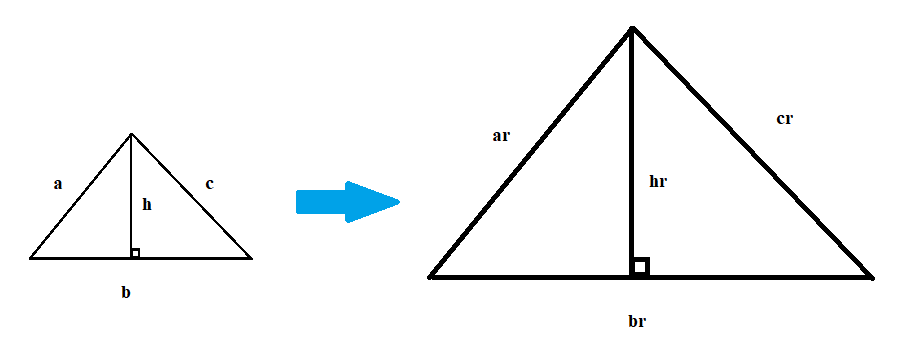
What's the area ratio now? Well, the first triangle has area \(\frac12bh\), and the second triangle has area \(\frac12(br)(hr)=\frac12bhr^2\). That means that the ratio between their two areas is \(\frac12bh:\frac12bhr^2\), which is the same ratio as \(1:r^2\). Ta-da!
You're probably wondering how you can prove this for all possible shapes. It's an interesting question to think about! See if you can come up with any good explanation as to why it would work for every shape you could draw.
Now, to finally answer the original question, we know that the triangles \(\triangle PCD\) and \(\triangle PAD\) are similar, and the ratio of their sides is \(9:15\). That means that \(\triangle PAD\) is \(\frac{15}{9}\) times bigger, or \(\frac{5}{3}\). So, by what we discussed, its area must be \(\frac{25}{9}\) bigger, and that's why the ratio of the areas is \(9:25\).
So in general, if you have two similar triangles with corresponding sides of ratio \(a:b\), then the ratio between the areas will be \(a^2:b^2\).
I hoped that helped. Be sure to let us know if you have more questions. Happy learning!
Thomas
-
Just wondering, how long does it take for you to make a single post? You seem to work a lot.
-
@bulba_bulbasaur
 I think maybe I spent 30 minutes on this particular post, most of which was spent making the diagrams. I really like making diagrams because, like the saying goes, "A picture is worth a thousand words..."
I think maybe I spent 30 minutes on this particular post, most of which was spent making the diagrams. I really like making diagrams because, like the saying goes, "A picture is worth a thousand words..." 
